(11.5)では本題とはしていなかったものを、本題に取り込むはなし。つまり本題のほうにも Basemap を採用する。ついでに pyproj も使う。
(11.5)でBasemapに期待したのは、緯度経度(線)の表示と海岸線表示、だった。けれど、本題のほうでは海岸線表示はどうでもよい。
義務教育レベルの話なので、本当は説明するまでもないことなんだけれど、経験上どうやら9割くらいのいい大人が「初耳です!」と驚くらしいことを軽く説明しとく。驚いて喜んでくれるならまだ良いのだが、最近は「知らないことが正義、教えないことが悪」とばかりに「どうして教えてくれないんですか」と、昔なら小学生にしか許されなかったようなことを当たり前に言う若者ばかりなので、一応。(義務教育レベルだと言ってる。けど、当人にとっては「忘れた」と「教わったことがない」が同義語だし、「教えてもらうのは当然の義務」として譲らないからさ。なんかね、もう、諦めるしかないのかなと思う。そういう時代だ。)
まず、「緯度と経度を基準に切り取った矩形は、場所によって大きさが違う」ことについて。こんな絵で感覚的にわかってちょ:
これ、中学の地理で習うはずなんだぜ? でもワタシのまわりの、何十人も、「思い出した、懐かしい、そういえば習った」という反応ならまだしも、怒り出す子までいて、参ったのよ、あたしゃ。どうも「難しいことはお前のせいだ」という怒りのスイッチ入るようで。たまらんわー。ほんと脳みそカチわって中身解析したいぞ。
さて。この理由、についても義務教育レベルね。「緯度・経度」というのが、地球をどう分割する線なのか。これを絵にしてみればすぐに理解出来る。経度方向の一度は、赤道で最大で、極でゼロになる。つまり、北極点に立てば、「全地球の全経度制覇」を数秒で実現出来る。
もう一つ、中学地理レベルの話。「メルカトル図法とか」と、キーワードを出せば辛うじて思い出してくれる人は良いほうで、それすら思い出してくれない人も多かった。要するに「球面を平面に展開する」という問題、正確な用語では「投影法(projection)」。丸まったものを平たくする問題なわけなんだけど、例えばテニスボールを押しつぶして判を取ってみることを想像してみるといい。転がすことなく「ボール全体」を押し付けることができないことはすぐにわかるはず。これを、「何を大事にして、何を捨てることによって実現するのか」によって、色んな投影法がある、というわけだね。面積を維持する、角度を維持する、距離を維持する。
ここまでは義務教育レベルで、高校以降の高等教育ではじめて教わるのが、「地球は真球ではない」といったことで、これは高校なら地学を選択しない限り教わらないだろうから、これを知らない大人がいてもまぁそんなには驚かない。(真球でないことによって、緯度一度の大きさも、緯度ごとに変化する。ただし、これは非常に小さな差で、経度の激変に較べればあまり問題にはならない。)
さて。この、義務教育レベルのものもそうでないものも、これが「理論と実現」の話になってくると、これはもう大学レベル。しかも教養レベルじゃない。地球科学系や宇宙科学系でも専攻しない限りは、まず知る機会はない。たとえばこんなだ。「球面三角法」なんか、言葉すら聞いたことがない人がほとんどだろう。けれども、これが「コンピュータソフトウェア上での実現」ということになると話は別で、これら非常に高度で難解な計算を行ってくれるインフラが、今では簡単に手に入る。それが、PROJ.4、GeoGraphicLib などであり、pyproj はこれら2つへのラッパーになっていて、かつ、Basemap も PROJ.4 に計算を委ねている。
なお、GEOS は GIS のもう一つの側面、「領域どうしの関係演算」(重なりの抽出など)を担うライブラリで、Basemap はこれにも依存し、また、GEOS, PROJ.4 は Postgis のバックエンドにもなっている。
さて。前置きはここまで。
今回何をしたいかというと、これまで「アスペクト比が…」と誤魔化していた問題を、Basemap で「ちゃんと」プロジェクションを扱うことで解決してしまおうと、そういうわけだ。ある程度の広域になってくると、北辺と南辺のスケールがかなり違うのに、「WEBメルカトル」ではそれを表現出来ない。それに Basemap 使えば緯度経度線も描画してくれるしね、いいじゃないの。
まずは本題の方に適用する前に、処理が軽い(11.5)の「done_vis.py」のレベルで十分に遊んでおく。こういうこと:
1 # -*- coding: utf-8 -*-
2 import os
3 import re
4 import numpy as np
5 import np_utils
6
7
8 # ##################################################
9 #
10 import datafile_tree
11
12
13 _all = np.zeros((135 * 8 * 10, 80 * 8 * 10))
14 for fn, dty, m1, m2, m3 in datafile_tree.walk("__converted"):
15 y = m1[0] * 8 * 10 + m2[0] * 10 + m3[0]
16 x = m1[1] * 8 * 10 + m2[1] * 10 + m3[1]
17 print(dty, m1, m2, m3, (y, x))
18 _all[y, x] += 2. if dty == "DEM05" else 1.
19
20 bd = np_utils.get_bound(_all, f=lambda a: a == 0.)
21 _x2lon = lambda x: x / (8 * 10.) + 100.
22 _y2lat = lambda y: y / (8 * 10.) * (2 / 3.)
23 elevs = _all[bd]
24 X = np.linspace(
25 _x2lon(bd[1].start),
26 _x2lon(bd[1].stop - 1),
27 elevs.shape[1])
28 Y = np.linspace(
29 _y2lat(bd[0].start),
30 _y2lat(bd[0].stop - 1),
31 elevs.shape[0])
32
33
34 # ##################################################
35 #
36 from mpl_toolkits.basemap import Basemap
37 import matplotlib.pyplot as plt
38 import matplotlib.cm as cm
39
40 fig = plt.figure()
41 fig.set_size_inches(16.53 * 2, 11.69 * 2)
42 m = Basemap(
43 llcrnrlon=X[0] - (X[10] - X[0]) / 2.,
44 llcrnrlat=Y[0] - (Y[10] - Y[0]) / 2.,
45 urcrnrlon=X[-1] + (X[2 * 10] - X[0]),
46 urcrnrlat=Y[-1],
47 resolution='f',
48 lat_0=(Y[0] + Y[-1]) / 2.,
49 lon_0=(X[0] + X[-1]) / 2.,
50 projection='cass')
51
52 lons, lats = np.meshgrid(X, Y)
53 x, y = m(lons, lats)
54
55 m.drawcoastlines(color='0.9', linewidth=1)
56 #m.fillcontinents(alpha=0.3)
57 circles = np.arange(10, 90, 0.5)
58 m.drawparallels(circles, labels=[1, 1, 1, 1])
59 meridians = np.arange(-180, 180, 0.5)
60 m.drawmeridians(meridians, labels=[1, 1, 1, 1])
61 m.pcolor(x, y, elevs, cmap=cm.summer)
62 plt.savefig("motterumotteru.png", bbox_inches="tight")
63 #plt.show()
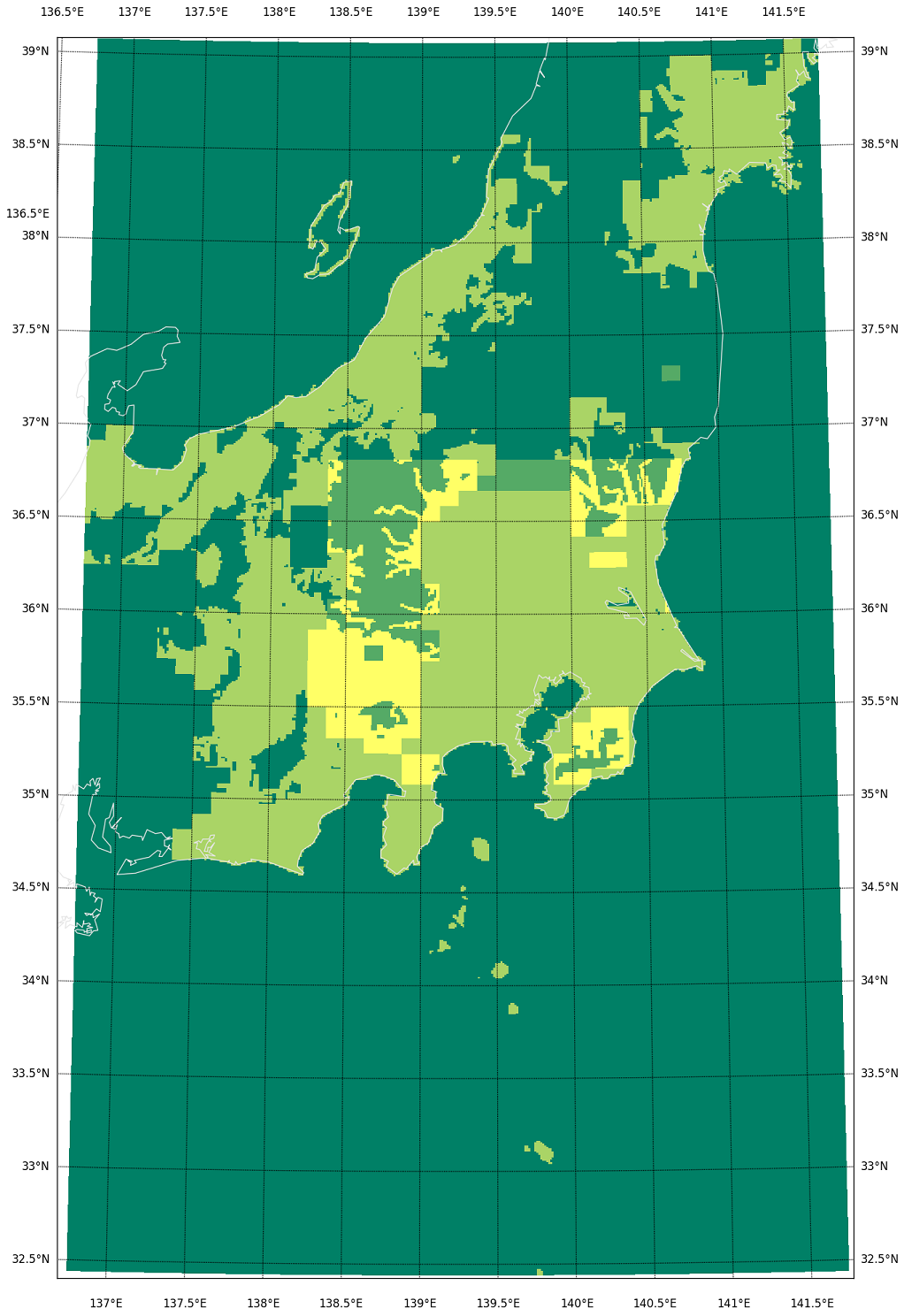
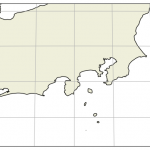
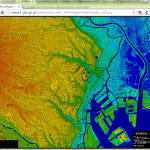
projection=’cass’ はCassini Projectionである。Cassini Projectionそのものを調べると「the central meridian からの距離を維持する」と説明されてると思うが、Basemap のはどうやら「(lon_0、lat_0で)指定した中心に先に回転」するみたい。やってみればすぐにわかることだけれど、データのある「緯度経度目線での矩形」が溢れてしまうので、43~46行目で、描画範囲の緯度経度を少し広げている。こんな結果:
Google Map ばかりに見慣れているとほとんどの人が気付かないが、これだけの広域になると、このように、かなりスケール差がある。(Google Map や地理院地図WEB で採用している投影法は「WEBメルカトル」。)ちょっと前にやった関東平野全域でも、小さくない差が出るが、これはのちほど実際にやってみる。
さて。「絵」としてはこれで満足、だが、実際この絵の「北端辺」と「南端辺」って、どれだけの距離差があるんだろうか? これを確かめるには、pyproj を使える。pyproj は PROJ.4 ラッパー部分と GeographicLib ラッパー部分が別物として分離されていて、後者の方が厳密な計算をする。ので、こちらを使ってみる:
1 from pyproj import Geod
2 g = Geod(ellps='WGS84')
3 # 地球楕円体のより正確な近似としてはGRS80(国際標準)がより良いとみなさ
4 # れているが、GPS によりデ・ファクトスタンダードとなったWGS84でも実用
5 # 上全く違いは出ない。(扁平率がほんの少しだけ違う。)
6 distH = g.inv(X[0], Y[-1], X[-1], Y[-1])[2]
7 distL = g.inv(X[0], Y[0], X[-1], Y[0])[2]
8 print("at lat=%.5f: %d[m]" % (Y[-1], distH))
9 print("at lat=%.5f: %d[m]" % (Y[0], distL))
あ、説明し忘れてた。「WGS84」とか「GRS80」の理解が、GIS 利用には不可欠なんだけれども、実用上はこのどちらか(大抵は WGS84)だけ知ってれば十分です。上で「地球は真球じゃない」と言ったけど、この「楕円っぷり」の表現の違いです。
で、Geod#inv は、「A地点からB地点まで」の、方位角(azimuth)と距離を計算してくれます。直線距離じゃないぞ。直線距離では地球内部を通っちゃうでしょう? そうじゃなくて、球面に沿った距離。結果はこれ:
1 at lat=39.07500: 431538[m]
2 at lat=32.44167: 468968[m]
この絵の最南端の緯度と、最北端の緯度の場合、WEBメルカトルでは同じ距離に見えていたのに、468,968 – 431,538 = 37.43 [km] も違うってこと。
ここまではよろしい? では、本題のほうに適用してみる。関東平野全域の標高図ね。結局こんな:
1 # -*- coding: utf-8 -*-
2 import numpy as np
3 import converted_loader
4 import sys
5 import logging
6 logging.basicConfig(
7 stream=sys.stdout, level=logging.INFO)
8 _logger = logging.getLogger(__name__)
9
10
11 lat_min = 34.590707
12 lat_max = 36.797053
13 lon_min = 138.488159
14 lon_max = 140.888895
15 #
16 _logger.info("lat_min = %.6f" % lat_min)
17 _logger.info("lat_max = %.6f" % lat_max)
18 _logger.info("lon_min = %.6f" % lon_min)
19 _logger.info("lon_max = %.6f" % lon_max)
20
21 X, Y, elevs = converted_loader.load_range(
22 lat_max, lon_max,
23 lat_min, lon_min)
24
25 elevs[np.isnan(elevs)] = np.nanmin(elevs)
26
27 #
28 import matplotlib
29 import matplotlib.cm as cm
30 import matplotlib.pyplot as plt
31 from mpl_toolkits.basemap import Basemap
32
33 fig, ax = plt.subplots()
34 fig.set_size_inches(16.53 * 2, 11.69 * 2)
35
36 from matplotlib.colors import LightSource
37 ls = LightSource(azdeg=180, altdeg=15)
38
39 m = Basemap(
40 llcrnrlon=X[0],
41 llcrnrlat=Y[0],
42 urcrnrlon=X[-1],
43 urcrnrlat=Y[-1],
44 resolution='c',
45 lat_0=(Y[0] + Y[-1]) / 2.,
46 lon_0=(X[0] + X[-1]) / 2.,
47 projection='cass', ax=ax)
48
49 #m.drawcoastlines(color='0.9', linewidth=1)
50 #m.fillcontinents(alpha=0.3)
51 circles = np.arange(10, 90, 0.25)
52 m.drawparallels(circles, labels=[1, 0, 0, 0])
53 meridians = np.arange(-180, 180, 0.25)
54 m.drawmeridians(meridians, labels=[0, 0, 0, 1])
55 #
56 rgb = ls.shade(elevs, cm.rainbow)
57 cs = m.imshow(elevs)
58 m.imshow(rgb)
59 m.colorbar(cs)
60
61 #
62 plt.savefig("kanto-heiya-cass.pdf", bbox_inches="tight")
63 #plt.show()
64 #
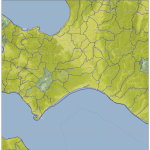
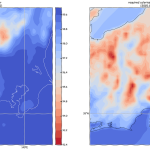
done_vis.py と同じノリで出来るのが理想だったんだけれども、そうはいかなかった。LightSource かけると、手にするのは rgb でしかなくて、これは imshow にしか渡せないんだけれど、そうすると、done_vis.py では渡せた(np.meshgrid で作ったもの) x, y を渡せない。これは何を意味するかと言うと、「m = Basemap(」で Basemap オブジェクトを作る際の llcrnrlon、llcrnrlat、urcrnrlon、urcrnrlat で与えた範囲に rgb 行列がぴったり収まる、ということを前提にしないといけない、ということ。ちょっとこれはイケてない。でもまぁ…:
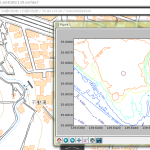
Click here to download
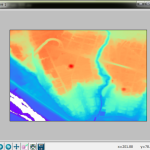
東経138.5度線に注目。これが一番わかりやすい。これを南から北に目で追っかけてみ。
まぁひとまずは目的を果たせた、ってことだけれども、ただねぇ、この投影法と「海だらけ領域を刈り取る」の相性がよろしくないのが一番気になる。刈り取り過ぎると Cassini Projection でデータ有効領域の端が欠けちゃうからね。うーん。まぁそのうち考えよう。
2021-05-07追記:
紹介した basemap だが、作者である Jeff Whitaker が「basemap プロジェクト」としての保守を完全にやめ、pip でのインストールも不可能になった。自身による説明:
Deprecation Notice
Basemap is deprecated in favor of the Cartopy project. See notes in Cartopy, New Management, and EoL Announcement for more details.
リンク先をちょっと読むに、「より大きなプロジェクトに取り込まれた」ということに見える。cartopy はワタシ自身にとって完全に未知なのでまだ何も言わないけれど、余力があったらそのうち何か書くかも。