馬鹿に徹するふりを一旦やめる。
(6)までの話ってのは、「専門家でないとわかるはずねーじゃん」的思考停止への警鐘、みたいなもんでね、「中学生レベルの理解が政治家に勝る、かもしらんよ」てことをば言いたかったわけなのよ。だからといって「それがいい、それが正しい」てのももちろん違う。「中学生レベルの素人理解も捨てたもんじゃない」のは、やってみせた通り、これは確か。だからといって、「理解できるから信頼できる」と思ってもらっては困る。
正直ワタシも感染症学的な専門的な話にはほとんどついていけない。そういう場合には、もちろん「専門家の意見を聞く」のが、態度として正しい。だから、ワタシとしては「素人理解」部分だけに済ませ、あまり深入りはしないつもりなんだけれど、少しだけわかることもあったので、ちょっとだけ。
csvを自分の都合のいいデータに加工するスクリプト(3)(週平均、二週平均、実効再生産数もついでに取ってる)
1 # -*- coding: utf-8 -*-
2 import io
3 import sys
4 import csv
5 import datetime
6 import numpy as np
7
8
9 def _tonpa(fn):
10 # rownum=2020/1/16からの日数, colnum=都道府県コード-1
11 result = {
12 "newpat": np.zeros((1, 47)),
13 "newpatmovavg": np.zeros((1, 47)), # 週平均
14 "newpatmovavg2": np.zeros((1, 47)), # 2週平均
15 "newdeath": np.zeros((1, 47)),
16 "newdeathmovavg": np.zeros((1, 47)),
17 "newdeathmovavg2": np.zeros((1, 47)),
18 "effrepro": np.zeros((1, 48)), # 実効再生産数(47都道府県+全国)
19 }
20 era = "2020/1/16"
21 era = datetime.datetime(*map(int, era.split("/")))
22 reader = csv.reader(io.open(fn, encoding="utf-8-sig"))
23 next(reader)
24 for row in reader:
25 dt, (p, c, d) = row[0], map(int, row[1::2])
26 dt = (datetime.datetime(*map(int, dt.split("/"))) - era).days
27 if dt > len(result["newpat"]) - 1:
28 for k in result.keys():
29 cn = 48 if k == "effrepro" else 47
30 result[k] = np.vstack((result[k], np.zeros((1, cn))))
31 result["newpat"][dt, p - 1] = c
32 result["newpatmovavg"][dt, p - 1] = result[
33 "newpat"][max(0, dt - 7):dt + 1, p - 1].mean()
34 result["newpatmovavg2"][dt, p - 1] = result[
35 "newpat"][max(0, dt - 14):dt + 1, p - 1].mean()
36 result["newdeath"][dt, p - 1] = d
37 result["newdeathmovavg"][dt, p - 1] = result[
38 "newdeath"][max(0, dt - 7):dt + 1, p - 1].mean()
39 result["newdeathmovavg2"][dt, p - 1] = result[
40 "newdeath"][max(0, dt - 14):dt + 1, p - 1].mean()
41 # 実効再生産数は、現京都大学西浦教授提案による簡易計算(を一般向け説明にまとめてくれ
42 # ている東洋経済ONLINE)より:
43 # （直近7日間の新規陽性者数／その前7日間の新規陽性者数）^（平均世代時間／報告間隔）
44 # 平均世代時間は=5日、報告間隔=7日の仮定。
45 # のつもりだが、東洋経済ONLINEで GitHub にて公開(閉鎖予定)されてる計算結果の csv とは
46 # 値が違う。違うことそのものは致し方ないこと。計算タイミングによって結果は変わるし、
47 # NHK まとめと東洋経済ONLINEのデータはシンクロしてないから。思いっきり間違ってるって
48 # ことはなさそう。近い値にはなってる。
49 for dt in range(len(result["newpat"])):
50 # 都道府県別
51 sum1 = result["newpat"][dt-6:dt+1, :47].sum(axis=0)
52 sum2 = result["newpat"][dt-6-7:dt+1-7, :47].sum(axis=0)
53 result["effrepro"][dt, :47] = np.power(sum1 / sum2, 5. / 7.)
54
55 # 全国
56 sum1 = result["newpat"][dt-6:dt+1, :].sum()
57 sum2 = result["newpat"][dt-6-7:dt+1-7, :].sum()
58 result["effrepro"][dt, 47] = np.power(sum1 / sum2, 5. / 7.)
59 np.savez(io.open("nhk_news_covid19_prefectures_daily_data.npz", "wb"), **result)
60
61
62 if __name__ == '__main__':
63 fn = "nhk_news_covid19_prefectures_daily_data.csv"
64 _tonpa(fn)
2021-02-02追記:
スクリプトをマジメに読んだ人は気付いたかもしれない。「8日平均」と「15日平均」を計算しちゃってる。一連の「主張」の本題とはあまり関係ないとはいえ、さすがにもうちょっと慎重にやるべきでした、すまぬ。正しくは「dt – 6」「dt – 5」…「dt – 1」「dt」の7エレメントでの平均を取らなければならないので、「slice(dt – 6, dt + 1)」。8日平均が役に立たないわけではないけれど、やりたいこととやってることが違うので、間違いは間違い。グラフは滑らかさが若干減って、もうほんの少しだけガタガタになる。
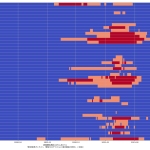
スクリプトをマジメに読んだ人は気付いたかもしれない。「8日平均」と「15日平均」を計算しちゃってる。一連の「主張」の本題とはあまり関係ないとはいえ、さすがにもうちょっと慎重にやるべきでした、すまぬ。正しくは「dt – 6」「dt – 5」…「dt – 1」「dt」の7エレメントでの平均を取らなければならないので、「slice(dt – 6, dt + 1)」。8日平均が役に立たないわけではないけれど、やりたいこととやってることが違うので、間違いは間違い。グラフは滑らかさが若干減って、もうほんの少しだけガタガタになる。
元にしたのは東洋経済ONLINEのデータまとめ。計算方法は元を正せば西浦教授提案のもの。
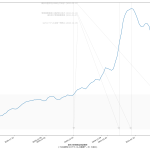
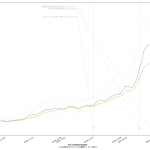
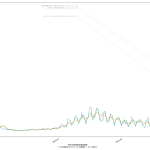
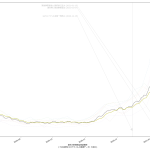
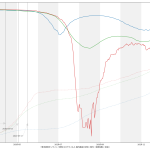
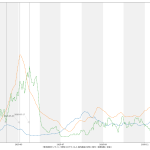
思ったのは、メディアはじめ多くの人々が、この「実効再生産数」の使い方を間違ってるのではないのかな、てこと。実に、(6)までの話と全く共通の話なんだが、「ある特定の一日の実効再生産数そのもの」だけをみるのって、これ、「予測してない」ことになるんだと思うんだ。Rt が 1未満になる、これは「収束」と言われている…、と思われてるフシがあって、めっちゃコワイ。そうじゃなくて、「Rt 1未満で推移すれば収束へ向かう」てことなわけ。だってこれ、感染者数でいえば「グラフの傾き」そのものだからね。
伝わるかなぁ。ある日「実効再生産数が1を下回った」場合に、「安心だ、もう動き回って大丈夫」と判断するのは絶対にダメで、「この実効再生産数が続けば～後に～人を下回るので～日後に動き回って大丈夫になる」と思考しなければならんでしょう、てこと。わかる?
たぶんこういうことだと思うんだよね:
上のスクリプトでセーブしたデータを読み込んでアホ予測と可視化を行うやーつ
1 # -*- coding: utf-8 -*-
2 import io
3 import datetime
4 import numpy as np
5 from scipy.optimize import curve_fit
6 import matplotlib as mpl
7 import matplotlib.pyplot as plt
8 import matplotlib.font_manager
9
10
11 def _vis(dat):
12 def _fcurve(t, a, b, c):
13 return a * np.power(t, b) + c
14
15 era = "2020/1/16"
16 era = datetime.datetime(*map(int, era.split("/")))
17 npat = dat["newpat"][:,12] # 12: 東京 (都道府県コード13)
18 npatma = dat["newpatmovavg"][:,12]
19 effrepro = dat["effrepro"][:,12]
20 #npat = dat["newpat"].sum(axis=1)
21 #npatma = dat["newpatmovavg"].sum(axis=1)
22 npatmadif = (npatma - np.roll(npatma, 1))
23 npatmadifacc = (npatmadif - np.roll(npatmadif, 1))
24
25 fontprop = matplotlib.font_manager.FontProperties(fname="c:/Windows/Fonts/meiryo.ttc")
26
27 T = [era + datetime.timedelta(t) for t in range(len(npat))]
28 #for t0 in range(0, len(T), 28):
29 for t0 in range(28, len(T) - 26):
30 tlast = min(len(T) - 1, t0 + 28)
31 cspan = slice(t0, tlast + 1)
32 pspan = slice(tlast, tlast + 7)
33
34 T2 = [era + datetime.timedelta(t) for t in range(pspan.start, pspan.stop)]
35 dtbeg, dtend = era + datetime.timedelta(t0), era + datetime.timedelta(tlast)
36 fig, ax1 = plt.subplots(tight_layout=True)
37 fig.set_size_inches(16.53, 11.69)
38 l2, = ax1.plot(T[cspan], npatma[cspan], color="blue")
39 # 予測1: 単に線形で延長
40 # 予測2: 二週前と前週の傾きの差を上積み
41 last = npatma[cspan][-1]
42 cdif = npatmadif[cspan.stop - 7:cspan.stop]
43 cdifacc = npatmadifacc[cspan.stop - 7:cspan.stop]
44 #
45 # 予測3: 「指数関数」への近似
46 # (予測日を起点としないので、グラフは不連続になる。)
47 tt0 = np.arange(cspan.start - t0, cspan.stop - t0)
48 popt, pcov = curve_fit(_fcurve, tt0, npatma[cspan])
49 tt1 = np.arange(tt0[-1], tt0[-1] + 7)
50 fc = _fcurve(tt1, *popt)
51 #
52 # 予測4: (西浦教授提案簡易計算による)実効再生産数で増加する予測。
53 # (一週間同じ値と仮定。)
54 er = effrepro[tlast]
55 #
56 #
57 prd0 = last
58 prd1 = max(0, last + cdif.mean() * 7)
59 prd2 = max(0, last + (cdif.mean() + cdifacc.mean()) * 7)
60 prd4 = last * er
61 l4, = ax1.plot(
62 T2, np.linspace(prd0, prd1 + 1, len(T2)), linestyle="dotted", color="black")
63 l5, = ax1.plot(
64 T2, np.linspace(prd0, prd2 + 1, len(T2)), linestyle="dotted", color="red")
65 l6, = ax1.plot(
66 T2, fc, linestyle="dotted", color="green")
67 l7, = ax1.plot(
68 T2, np.linspace(prd0, prd4 + 1, len(T2)), linestyle="dotted", color="orange")
69
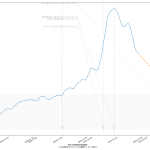
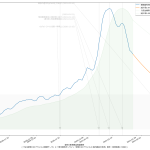
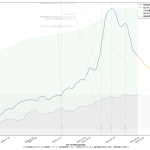
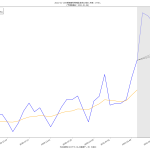
70 tit = """{}の新規陽性判明数週平均(東京)の素人予測: 予測1={}人, 予測2={}人, 予測3={}人, 予測4(実効再生産数={:.2f})={}人
71 (予測実施日: {})""".format(
72 str(dtend + datetime.timedelta(7)).partition(" ")[0],
73 int(prd1), int(prd2), int(fc[-1]), er, int(prd4), str(dtend).partition(" ")[0])
74 ax1.set_title(tit, fontproperties=fontprop)
75 l3, = ax1.plot(T2[:len(npatma[pspan])], npatma[pspan], color="blue", alpha=0.2)
76 ax1.legend(
77 (l2, l4, l5, l6, l7),
78 ("新規陽性判明数週平均", "新規陽性判明数週平均予測1",
79 "新規陽性判明数週平均予測2", "新規陽性判明数週平均予測3",
80 "新規陽性判明数週平均予測4"),
81 shadow=True, prop=fontprop)
82 ax1.set_xlabel("「NHK新型コロナウイルス関連データ」を加工", fontproperties=fontprop)
83 plt.axvspan(T2[0], T2[-1], facecolor="lightgray", alpha=0.5)
84 fig.autofmt_xdate()
85 fig.savefig("result/{:04d}.png".format(t0))
86 #plt.show()
87 plt.close(fig)
88
89
90 if __name__ == '__main__':
91 fn = "nhk_news_covid19_prefectures_daily_data.npz"
92 _vis(np.load(io.open(fn, "rb")))
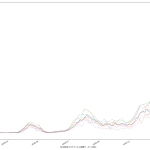
実効再生産数が1.0の場合に、今日が新規感染者100人で明日も100人となる、2.0の場合は200人になる、という計算にしてるけど、それで正しいのかどうかがイマイチよくわからない。それっぽい感じにはなってるとは思うけど。はっきりいって、こういうのこそ専門家にやって欲しい。つまりこの予測そのものは一切信頼しないで欲しい。
ワタシが言いたいのは、一般向けに実効再生産数そのものに目を向けさせるのをやめ、「実効再生産数に基づく未来予測」で議論するようになるべきである、てことね。実際専門家、特に西浦さんがやってるのがまさにそれだけれど、毎日報道されるわけではないのが問題。最低でも、言ったように「実効再生産数が今日1.0を下回ったので今日おk、明日から自由だぁ」という考えを誘発させる見せ方は今すぐやめること。だと思うんだけどね。
