ついでなので。
前々回、前回のは、「中学生でも理解出来、筆算ですら実現出来るほど単純」それと言い足りなかったが「なので誰でもすぐに納得できる」という理由でもって、メディアは毎日自前でもいいので近未来予想を報道したらいいんでわ、というのが趣旨であった。
ここで話をやめてもいいんだけれど、ついでなので、「もう一歩だけ」話を進めてみる。
わかる人はわかる、のかもしんないんだけれど、ワタシは「脳内でこの計算を実はやってる」と言っときながら、ほんとは全然「線形に延長」なんてやってない。二つ目でやった増加率の加味まで大抵やってる、という言い方でもいいんだけれど、「教科書的には、感染症の感染者は指数関数的に増加する」ということを知っているので、脳内では実際は指数関数を前提に曲線を引いてる。「感染症の感染者は」ということに納得できない人は「鼠算」を思い出せばいい。もしくは「倍々ゲーム」ね。
これはさすがに「指数関数」が高校数学レベルであるうえに、これへの近似となると、理系の大学教養レベルですらなくて、「理系の専門課程の初期」くらいのレベル。筆算が不可能とは言わないが、当然コンピュータの力を借りることが普通は前提になる。
この近似が簡単に出来るかどうかは、もってる道具次第。MS Excel もそれなりにフィテッィング機能があるはずだけど、ワタシの PC に入ってないので確認出来ない。Python で計算する場合は、scipy を使うのが簡単。こんなだね:
1 # -*- coding: utf-8 -*-
2 import io
3 import sys
4 import csv
5 import datetime
6 import numpy as np
7
8
9 def _tonpa(fn):
10 # rownum=2020/1/16からの日数, colnum=都道府県コード-1
11 result = {
12 "newpat": np.zeros((1, 47)),
13 "newpatmovavg": np.zeros((1, 47)),
14 "newdeath": np.zeros((1, 47)),
15 "newdeathmovavg": np.zeros((1, 47)),
16 }
17 era = "2020/1/16"
18 era = datetime.datetime(*map(int, era.split("/")))
19 reader = csv.reader(io.open(fn, encoding="utf-8-sig"))
20 next(reader)
21 for row in reader:
22 dt, (p, c, d) = row[0], map(int, row[1::2])
23 dt = (datetime.datetime(*map(int, dt.split("/"))) - era).days
24 if dt > len(result["newpat"]) - 1:
25 for k in result.keys():
26 result[k] = np.vstack((result[k], np.zeros((1, 47))))
27 result["newpat"][dt, p - 1] = c
28 result["newpatmovavg"][dt, p - 1] =
29 result["newpat"][max(0, dt - 7):dt + 1, p - 1].mean()
30 result["newdeath"][dt, p - 1] = d
31 result["newdeathmovavg"][dt, p - 1] =
32 result["newdeath"][max(0, dt - 7):dt + 1, p - 1].mean()
33 np.savez(io.open("nhk_news_covid19_prefectures_daily_data.npz", "wb"), **result)
34
35
36 if __name__ == '__main__':
37 fn = "nhk_news_covid19_prefectures_daily_data.csv"
38 _tonpa(fn)
スクリプトをマジメに読んだ人は気付いたかもしれない。「8日平均」を計算しちゃってる。一連の「主張」の本題とはあまり関係ないとはいえ、さすがにもうちょっと慎重にやるべきでした、すまぬ。正しくは「dt – 6」「dt – 5」…「dt – 1」「dt」の7エレメントでの平均を取らなければならないので、「slice(dt – 6, dt + 1)」。8日平均が役に立たないわけではないけれど、やりたいこととやってることが違うので、間違いは間違い。グラフは滑らかさが若干減って、もうほんの少しだけガタガタになる。
1 # -*- coding: utf-8 -*-
2 import io
3 import datetime
4 import numpy as np
5 from scipy.optimize import curve_fit
6 import matplotlib as mpl
7 import matplotlib.pyplot as plt
8 import matplotlib.font_manager
9
10
11 def _vis(dat):
12 def _fcurve(t, a, b, c):
13 return a * np.power(t, b) + c
14
15 era = "2020/1/16"
16 era = datetime.datetime(*map(int, era.split("/")))
17 npat = dat["newpat"][:,12] # 12: 東京 (都道府県コード13)
18 npatma = dat["newpatmovavg"][:,12]
19 #npat = dat["newpat"].sum(axis=1)
20 #npatma = dat["newpatmovavg"].sum(axis=1)
21 npatmadif = (npatma - np.roll(npatma, 1))
22 npatmadifacc = (npatmadif - np.roll(npatmadif, 1))
23
24 fontprop = matplotlib.font_manager.FontProperties(fname="c:/Windows/Fonts/meiryo.ttc")
25
26 T = [era + datetime.timedelta(t) for t in range(len(npat))]
27 #for t0 in range(0, len(T), 28):
28 for t0 in range(28, len(T) - 26):
29 tlast = min(len(T) - 1, t0 + 28)
30 cspan = slice(t0, tlast + 1)
31 pspan = slice(tlast, tlast + 7)
32
33 T2 = [era + datetime.timedelta(t) for t in range(pspan.start, pspan.stop)]
34 dtbeg, dtend = era + datetime.timedelta(t0), era + datetime.timedelta(tlast)
35 fig, ax1 = plt.subplots(tight_layout=True)
36 fig.set_size_inches(16.53, 11.69)
37 l2, = ax1.plot(T[cspan], npatma[cspan], color="blue")
38 # 予測1: 単に線形で延長
39 # 予測2: 二週前と前週の傾きの差を上積み
40 last = npatma[cspan][-1]
41 cdif = npatmadif[cspan.stop - 7:cspan.stop]
42 cdifacc = npatmadifacc[cspan.stop - 7:cspan.stop]
43 #
44 # 予測3: 「指数関数」への近似
45 # (予測日を起点としないので、グラフは不連続になる。)
46 tt0 = np.arange(cspan.start - t0, cspan.stop - t0)
47 popt, pcov = curve_fit(_fcurve, tt0, npatma[cspan])
48 tt1 = np.arange(tt0[-1], tt0[-1] + 7)
49 fc = _fcurve(tt1, *popt)
50 #
51 prd0 = last
52 prd1 = max(0, last + cdif.mean() * 7)
53 prd2 = max(0, last + (cdif.mean() + cdifacc.mean()) * 7)
54 l4, = ax1.plot(
55 T2, np.linspace(prd0, prd1 + 1, len(T2)), linestyle="dotted", color="black")
56 l5, = ax1.plot(
57 T2, np.linspace(prd0, prd2 + 1, len(T2)), linestyle="dotted", color="red")
58 l6, = ax1.plot(
59 T2, fc, linestyle="dotted", color="green")
60
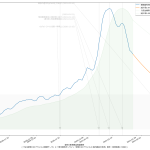
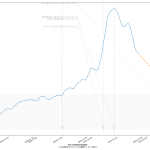
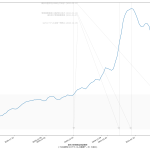
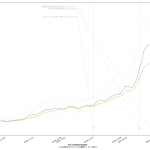
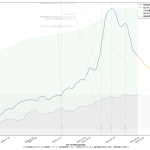
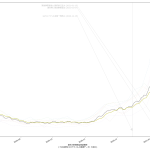
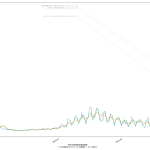
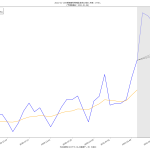
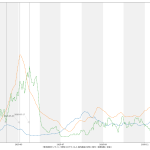
61 tit = """{}の新規陽性判明数週平均(東京)の素人予測: 予測1={}人, 予測2={}人, 予測3={}人
62 (予測実施日: {})""".format(
63 str(dtend + datetime.timedelta(7)).partition(" ")[0],
64 int(prd1), int(prd2), int(fc[-1]), str(dtend).partition(" ")[0])
65 ax1.set_title(tit, fontproperties=fontprop)
66 l3, = ax1.plot(T2[:len(npatma[pspan])], npatma[pspan], color="blue", alpha=0.2)
67 ax1.legend(
68 (l2, l4, l5, l6),
69 ("新規陽性判明数週平均", "新規陽性判明数週平均予測1",
70 "新規陽性判明数週平均予測2", "新規陽性判明数週平均予測3"),
71 shadow=True, prop=fontprop)
72 ax1.set_xlabel("「NHK新型コロナウイルス関連データ」を加工", fontproperties=fontprop)
73 plt.axvspan(T2[0], T2[-1], facecolor="lightgray", alpha=0.5)
74 fig.autofmt_xdate()
75 fig.savefig("result/{:04d}.png".format(t0))
76 #plt.show()
77 plt.close(fig)
78
79
80 if __name__ == '__main__':
81 fn = "nhk_news_covid19_prefectures_daily_data.npz"
82 _vis(np.load(io.open(fn, "rb")))
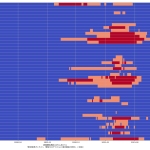
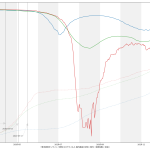
寄せる関数が単調増加関数なので、当然そうでない範囲、つまり山の頂上か谷底を含む場合はおかしな予測になる。まぁちゃんとしたいんなら、単調増加・単調減少となってる範囲を切り取って、その部分だけを近似するしかないわな。
(1)(2)については「中学生でもわかる簡単な計算なので」が、中学生が納得するのに寄与すると考えるかどうかはほんとは微妙で、「そんなバカな計算、当たるわけねーじゃんヴぁーかヴぁーか」と言われればその通り、そうした向きに「納得してもらう」には、「言葉」が必要である。たとえば「単純計算で」と冠するだけでも納得感が変わるかもしれない。じゃぁ今回の(3)はどうなのか、についてもほんとは大差はない。そうなのだけれども、「指数関数的に増える」という現象はこれは日常的にも良く知られた事象であり、言うほど一般市民に受け容れられない考え方でもないというのが結構大きく、また、ビデオで一致率が高い箇所を見てもらってもわかる通り、「わぉ、ほんとに指数関数ってら」となる、現実の感染症の感染数推移は。そりゃそうなのよ、倍々ゲームに「100%でない確率」が入ってるだけ、てことだからね。
つまり「ほんとに教科書どおり指数関数的に増加するとしたら」という予測は、まさに「最悪の想定」として提供するものとしては「ちゃんと相応しい」てこと。まぁ言った通りこれは「誰でも簡単に計算実施出来る」てもんではないとは思うんだけどさ、ただね、これに書いたように、少なくともワタシがはじめてプログラミングをまともにやり始めた20数年前と比較すると「難しい数学計算」が何百倍も簡単に誰でも出来うるようにはなってるんだよね。ワタシなら Python でだし、そうでないツールも結構あると思う。NHK の COVID19 サイトなんかもきっとどこかの IT 業者に外注するなりしてるんではないかと思うんだけど、そうしたエンジニアがこれら計算を専門家に頼らず仕込むことって、今はそんなに難しいことではないと思うのよね。やってみてもいいんじゃないのかなぁと。