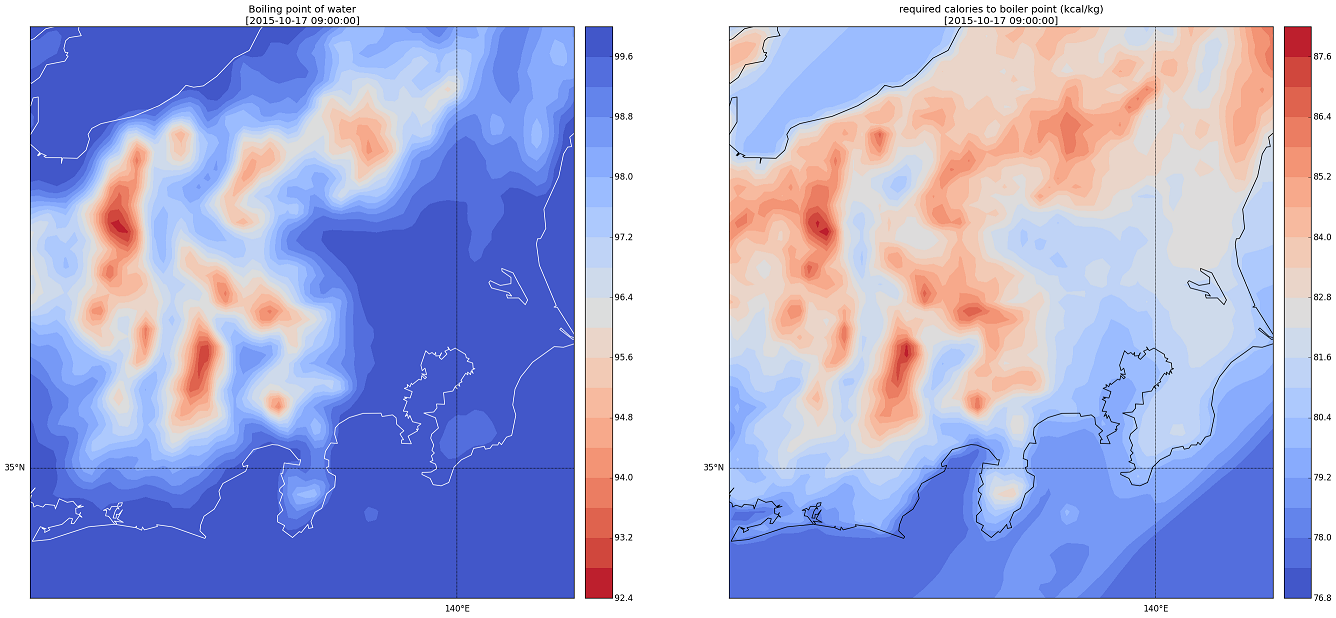
お遊びの上塗り。
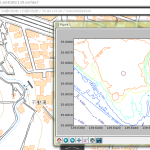
沸点がわかるとすれば、水が外気温と同じ水温と仮定して、この水温から沸点まで上げるのに必要なカロリーがわかる:
1 # -*- coding: utf-8 -*-
2 import sys
3 import pygrib
4 import numpy as np
5
6
7 def _read(srcfn):
8 # keys in Surfece:
9 # Pressure reduced to MSL
10 # Surface pressure
11 # 10 metre U wind component
12 # 10 metre V wind component
13 # Temperature
14 # Relative humidity
15 # Low cloud cover
16 # Medium cloud cover
17 # High cloud cover
18 # Total cloud cover
19 # Total precipitation
20 #
21 src = pygrib.open(srcfn)
22 for s in src:
23 yield (s.name, s.parameterName), s.validDate, s.latlons(), s.values
24 src.close()
25
26
27 data = {}
28 for yk, vd, latlons, values in _read(sys.argv[1]):
29 if "Pressure reduced to MSL" in yk and "Pressure reduced to MSL" not in data:
30 data["Pressure reduced to MSL"] = latlons, values
31 elif "Surface pressure" in yk and "Surface pressure" not in data:
32 data["Surface pressure"] = latlons, values
33 elif "Temperature" in yk and "Temperature" not in data:
34 data["Temperature"] = latlons, values
35 if len(data) == 3:
36 break
37
38
39 # -----------------------------------------------------
40 #
41 from mpl_toolkits.basemap import Basemap
42 import matplotlib.pyplot as plt
43 import matplotlib.cm as cm
44 import matplotlib.ticker as ticker
45
46
47 bmparams = dict(
48 llcrnrlat=34.25,
49 urcrnrlat=37.5,
50 llcrnrlon=137.,
51 urcrnrlon=140.825,
52 resolution='i',
53 projection='merc')
54
55 fig, axes = plt.subplots(1, 2)
56 fig.set_size_inches(16.53 * 2, 11.69 * 2)
57
58 circles = np.arange(10, 90, 5)
59 meridians = np.arange(-180, 180, 5)
60 # -----------------------------------------------------
61 # surface pressure as saturated vapour pressure
62 latlons, e_s = data["Surface pressure"]
63
64 # inverse of Murray's equation
65 ln_es = np.log(e_s / 100. / 6.1078)
66 T_B = 273.15 + (-ln_es * 237.3) / (ln_es - 17.2693882)
67
68
69 lons = latlons[1]
70 lats = latlons[0]
71 #
72 X = latlons[1][0,:]
73 Y = latlons[0][:,0]
74 bmparams["ax"] = axes[0]
75 m = Basemap(**bmparams)
76 x, y = m(lons, lats)
77 m.drawcoastlines(color='white', linewidth=1)
78 m.drawparallels(circles, labels=[1, 0, 0, 0])
79 m.drawmeridians(meridians, labels=[0, 0, 0, 1])
80
81 cs = m.contourf(
82 x, y,
83 T_B - 273.15, # K to Celsius
84 20,
85 cmap=cm.coolwarm_r)
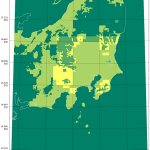
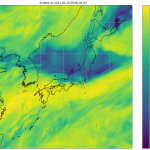
86 m.colorbar(cs)
87 axes[0].set_title("Boiling point of water\n[" + str(vd) + "]")
88 # -----------------------------------------------------
89 #
90 # temperature
91 latlons, T = data["Temperature"]
92
93 bmparams["ax"] = axes[1]
94 m = Basemap(**bmparams)
95 x, y = m(lons, lats)
96 m.drawcoastlines(color='black', linewidth=1)
97 m.drawparallels(circles, labels=[1, 0, 0, 0])
98 m.drawmeridians(meridians, labels=[0, 0, 0, 1])
99
100 #
101 cs = m.contourf(
102 x, y,
103 T_B - T,
104 20,
105 cmap=cm.coolwarm)
106 m.colorbar(
107 cs,
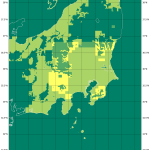
108 format=ticker.FuncFormatter(lambda x, pos: "%.1f" % x))
109 axes[1].set_title("required calories to boiler point (kcal/kg)\n[" + str(vd) + "]")
110 # -----------------------------------------------------
111 #plt.show()
112 plt.savefig("boiling_point_of_water2.png", bbox_inches="tight")
ちなみに水の比熱を調べたのは、水1度上げるのに必要なエネルギーが何かに依存して変化するんだったっけか、てのを知りたくて調べようとしたの。変わらない、でいいんだっけか。不変なら、ここでやった通り、「水1gを1℃上げるのに必要なカロリーは1cal (1kgを1℃、で1kcal)」。(1kg ≒ 1リットル、ね。)
標高が高い場所では、「100℃にはならないわ、余計にカロリー必要だわ」で踏んだり蹴ったり、の巻。
以前水の煮沸の話で国際山岳連合医療部会(UIAA MedCom)公認基準の話をちょっと紹介した。滅菌・殺菌のために必要なのは沸騰ではなく温度だけれども、沸騰でほぼ死滅させることは出来る。UIAA MedCom の「煮沸のデメリット」として「水を沸騰させるために燃料と時間を消費する」と言っているが、平地より余計にエネルギーが必要だ、ってわけ。
あ、「水温が外気温と同じ」はかなり無理がある仮定よ。例えば登山ならそんな水の運搬したら命に関わるし、平地の水道水は、おそらく浄水場の水温が保たれてるはず。水の比熱が高いから、ね。外気温の影響受けにくい。
2021-05-07追記:
紹介した basemap だが、作者である Jeff Whitaker が「basemap プロジェクト」としての保守を完全にやめ、pip でのインストールも不可能になった。自身による説明:
Deprecation Notice
Basemap is deprecated in favor of the Cartopy project. See notes in Cartopy, New Management, and EoL Announcement for more details.
リンク先をちょっと読むに、「より大きなプロジェクトに取り込まれた」ということに見える。cartopy はワタシ自身にとって完全に未知なのでまだ何も言わないけれど、余力があったらそのうち何か書くかも。