既に人さまの優秀なものがあって、別に不満があるということではなくて。
2019-01-01: 末尾の追記参照。
オレ式「音階と周波数の対応表」(一応)
ちょいと今個人的に不可思議なことに出くわしてしまっていて、どうしても色んな種類の検証方法が必要なんだけれど、そのうちの一つとして、やはりシンプルな対応表をいつでも手にしたい、ということ。
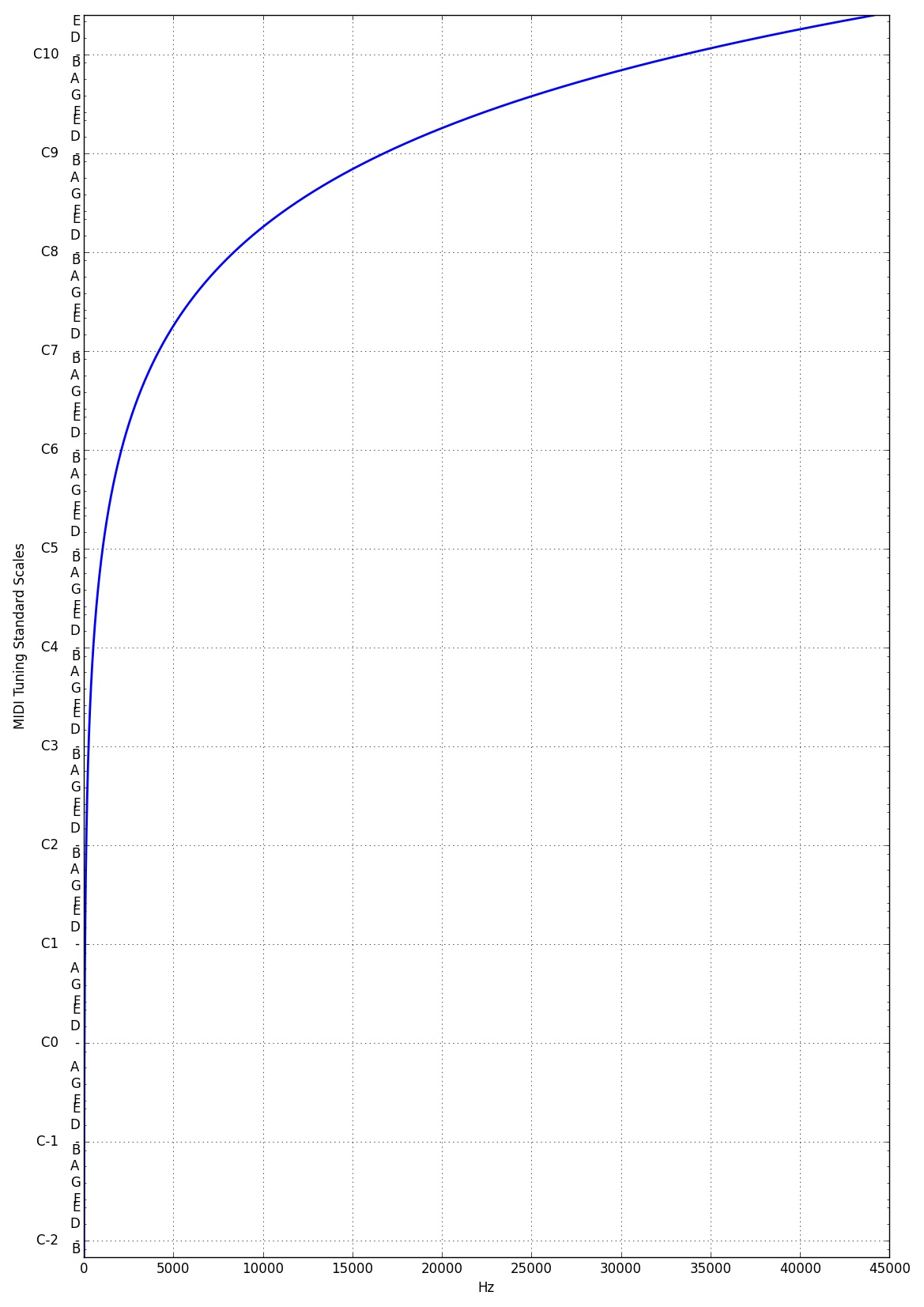
「FFT なスペクトラム可視化に音階をくっつけて(3)」で、「「log2 スケール的なこと」を、実はやるだけやってみた。」と言うだけ言って書き残さなかったもんで、自分でももう一度書くハメになったてのもあり、ただの表とその「「log2 スケール的なこと」グラフの両方をば:
1 import numpy as np
2
3
4 #
5 # see details: https://en.wikipedia.org/wiki/MIDI_tuning_standard
6 #
7 _SCALES_L = ["C", "C#/Db", "D", "D#/Eb", "E", "F", "F#/Gb", "G", "G#/Ab", "A", "A#/Bb", "B"]
8
9 def _nn2scale(d):
10 return int(d / 12) - 2, _SCALES_L[int(d) % 12]
11
12 def _nn2freq(d):
13 return np.power(2, (d - 69) / 12.) * 440
14
15 def _freq2nn(f):
16 return 69 + 12 * np.log2(f / 440.)
17
18 #############################################################
19 #
20 # matplotlib's custom scale implementation for MTS scales.
21 #
22 from numpy import ma
23 from matplotlib import scale as mscale
24 from matplotlib import transforms as mtransforms
25 import matplotlib.ticker as ticker
26
27
28 class MTSScaleScale(mscale.ScaleBase):
29 name = 'midituningstandardscale'
30
31 def __init__(self, axis, **kwargs):
32 mscale.ScaleBase.__init__(self)
33
34 def get_transform(self):
35 return self.MTSScaleTransform()
36
37 def set_default_locators_and_formatters(self, axis):
38 class _nnformat(ticker.Formatter):
39 def __init__(self, minor):
40 ticker.Formatter.__init__(self)
41 if minor:
42 self._fmt = lambda oc, sc: sc
43 else:
44 self._fmt = lambda oc, sc: "%s%d -" % (sc, oc)
45
46 def __call__(self, f, pos=None):
47 if f > 0:
48 nn = _freq2nn(f)
49 if nn - int(nn) < 1e-2:
50 oc, sc = _nn2scale(nn)
51 return self._fmt(oc, sc)
52 return ""
53
54 _all = np.arange(-24, 168)
55 _maj = np.array([v for v in _all if v % 12 == 0])
56 _min = np.array([v for v in _all if v % 12 in (2, 4, 5, 7, 9, 11)])
57 axis.set_major_locator(ticker.FixedLocator(_nn2freq(_maj)))
58 axis.set_minor_locator(ticker.FixedLocator(_nn2freq(_min)))
59 axis.set_major_formatter(ticker.FuncFormatter(_nnformat(False)))
60 axis.set_minor_formatter(ticker.FuncFormatter(_nnformat(True)))
61
62 def limit_range_for_scale(self, vmin, vmax, minpos):
63 return max(_nn2freq(-2), vmin), max(_nn2freq(-2), vmax)
64
65 class MTSScaleTransform(mtransforms.Transform):
66 input_dims = 1
67 output_dims = 1
68 is_separable = True
69
70 def __init__(self):
71 mtransforms.Transform.__init__(self)
72
73 def transform_non_affine(self, f):
74 masked = ma.masked_where((f == 0), f)
75 if masked.mask.any():
76 return 69 + 12 * ma.log2(f / 440.)
77 else:
78 return 69 + 12 * np.log2(f / 440.)
79
80 def inverted(self):
81 return MTSScaleScale.InvertedMTSScaleTransform()
82
83 class InvertedMTSScaleTransform(mtransforms.Transform):
84 input_dims = 1
85 output_dims = 1
86 is_separable = True
87
88 def __init__(self):
89 mtransforms.Transform.__init__(self)
90
91 def transform_non_affine(self, d):
92 return _nn2freq(d)
93
94 def inverted(self):
95 return MTSScaleScale.MTSScaleTransform()
96
97 mscale.register_scale(MTSScaleScale)
98 #############################################################
99
100 if __name__ == '__main__':
101 # to display as text
102 print("<table>")
103 print("<thead><tr><th>Note Number</th><th>Scale + Octave</th><th>Freq. (in Hz)</th></td></thead>")
104 for i in range(0, 132, 12):
105 for d in range(i, i + 12):
106 print("<tr><td>{:3d}</td><td>{:5s}{:-2d}</td><td>{:8.2f}</td></tr>".format(
107 d, _SCALES_L[d % 12], d // 12 - 2, _nn2freq(d)))
108 print("</table>")
109
110 # graphical display
111 import matplotlib.pyplot as plt
112 f = np.arange(44100)
113
114 fig, ax = plt.subplots()
115 fig.set_size_inches(11.69, 16.53)
116 ax.plot(f, f, '-', lw=2)
117 ax.set_yscale('midituningstandardscale')
118 ax.grid(True)
119
120 ax.set_xlabel("Hz")
121 ax.set_ylabel("MIDI Tuning Standard Scales")
122 #plt.show()
123 fig.tight_layout()
124 fig.savefig("MTS_Scales.jpg")
表のほうはこんな具合:
| Note Number | Scale + Octave | Freq. (in Hz) |
|---|---|---|
| 0 | C -2 | 8.18 |
| 1 | C#/Db-2 | 8.66 |
| 2 | D -2 | 9.18 |
| 3 | D#/Eb-2 | 9.72 |
| 4 | E -2 | 10.30 |
| 5 | F -2 | 10.91 |
| 6 | F#/Gb-2 | 11.56 |
| 7 | G -2 | 12.25 |
| 8 | G#/Ab-2 | 12.98 |
| 9 | A -2 | 13.75 |
| 10 | A#/Bb-2 | 14.57 |
| 11 | B -2 | 15.43 |
| 12 | C -1 | 16.35 |
| 13 | C#/Db-1 | 17.32 |
| 14 | D -1 | 18.35 |
| 15 | D#/Eb-1 | 19.45 |
| 16 | E -1 | 20.60 |
| 17 | F -1 | 21.83 |
| 18 | F#/Gb-1 | 23.12 |
| 19 | G -1 | 24.50 |
| 20 | G#/Ab-1 | 25.96 |
| 21 | A -1 | 27.50 |
| 22 | A#/Bb-1 | 29.14 |
| 23 | B -1 | 30.87 |
| 24 | C 0 | 32.70 |
| 25 | C#/Db 0 | 34.65 |
| 26 | D 0 | 36.71 |
| 27 | D#/Eb 0 | 38.89 |
| 28 | E 0 | 41.20 |
| 29 | F 0 | 43.65 |
| 30 | F#/Gb 0 | 46.25 |
| 31 | G 0 | 49.00 |
| 32 | G#/Ab 0 | 51.91 |
| 33 | A 0 | 55.00 |
| 34 | A#/Bb 0 | 58.27 |
| 35 | B 0 | 61.74 |
| 36 | C 1 | 65.41 |
| 37 | C#/Db 1 | 69.30 |
| 38 | D 1 | 73.42 |
| 39 | D#/Eb 1 | 77.78 |
| 40 | E 1 | 82.41 |
| 41 | F 1 | 87.31 |
| 42 | F#/Gb 1 | 92.50 |
| 43 | G 1 | 98.00 |
| 44 | G#/Ab 1 | 103.83 |
| 45 | A 1 | 110.00 |
| 46 | A#/Bb 1 | 116.54 |
| 47 | B 1 | 123.47 |
| 48 | C 2 | 130.81 |
| 49 | C#/Db 2 | 138.59 |
| 50 | D 2 | 146.83 |
| 51 | D#/Eb 2 | 155.56 |
| 52 | E 2 | 164.81 |
| 53 | F 2 | 174.61 |
| 54 | F#/Gb 2 | 185.00 |
| 55 | G 2 | 196.00 |
| 56 | G#/Ab 2 | 207.65 |
| 57 | A 2 | 220.00 |
| 58 | A#/Bb 2 | 233.08 |
| 59 | B 2 | 246.94 |
| 60 | C 3 | 261.63 |
| 61 | C#/Db 3 | 277.18 |
| 62 | D 3 | 293.66 |
| 63 | D#/Eb 3 | 311.13 |
| 64 | E 3 | 329.63 |
| 65 | F 3 | 349.23 |
| 66 | F#/Gb 3 | 369.99 |
| 67 | G 3 | 392.00 |
| 68 | G#/Ab 3 | 415.30 |
| 69 | A 3 | 440.00 |
| 70 | A#/Bb 3 | 466.16 |
| 71 | B 3 | 493.88 |
| 72 | C 4 | 523.25 |
| 73 | C#/Db 4 | 554.37 |
| 74 | D 4 | 587.33 |
| 75 | D#/Eb 4 | 622.25 |
| 76 | E 4 | 659.26 |
| 77 | F 4 | 698.46 |
| 78 | F#/Gb 4 | 739.99 |
| 79 | G 4 | 783.99 |
| 80 | G#/Ab 4 | 830.61 |
| 81 | A 4 | 880.00 |
| 82 | A#/Bb 4 | 932.33 |
| 83 | B 4 | 987.77 |
| 84 | C 5 | 1046.50 |
| 85 | C#/Db 5 | 1108.73 |
| 86 | D 5 | 1174.66 |
| 87 | D#/Eb 5 | 1244.51 |
| 88 | E 5 | 1318.51 |
| 89 | F 5 | 1396.91 |
| 90 | F#/Gb 5 | 1479.98 |
| 91 | G 5 | 1567.98 |
| 92 | G#/Ab 5 | 1661.22 |
| 93 | A 5 | 1760.00 |
| 94 | A#/Bb 5 | 1864.66 |
| 95 | B 5 | 1975.53 |
| 96 | C 6 | 2093.00 |
| 97 | C#/Db 6 | 2217.46 |
| 98 | D 6 | 2349.32 |
| 99 | D#/Eb 6 | 2489.02 |
| 100 | E 6 | 2637.02 |
| 101 | F 6 | 2793.83 |
| 102 | F#/Gb 6 | 2959.96 |
| 103 | G 6 | 3135.96 |
| 104 | G#/Ab 6 | 3322.44 |
| 105 | A 6 | 3520.00 |
| 106 | A#/Bb 6 | 3729.31 |
| 107 | B 6 | 3951.07 |
| 108 | C 7 | 4186.01 |
| 109 | C#/Db 7 | 4434.92 |
| 110 | D 7 | 4698.64 |
| 111 | D#/Eb 7 | 4978.03 |
| 112 | E 7 | 5274.04 |
| 113 | F 7 | 5587.65 |
| 114 | F#/Gb 7 | 5919.91 |
| 115 | G 7 | 6271.93 |
| 116 | G#/Ab 7 | 6644.88 |
| 117 | A 7 | 7040.00 |
| 118 | A#/Bb 7 | 7458.62 |
| 119 | B 7 | 7902.13 |
| 120 | C 8 | 8372.02 |
| 121 | C#/Db 8 | 8869.84 |
| 122 | D 8 | 9397.27 |
| 123 | D#/Eb 8 | 9956.06 |
| 124 | E 8 | 10548.08 |
| 125 | F 8 | 11175.30 |
| 126 | F#/Gb 8 | 11839.82 |
| 127 | G 8 | 12543.85 |
| 128 | G#/Ab 8 | 13289.75 |
| 129 | A 8 | 14080.00 |
| 130 | A#/Bb 8 | 14917.24 |
| 131 | B 8 | 15804.27 |
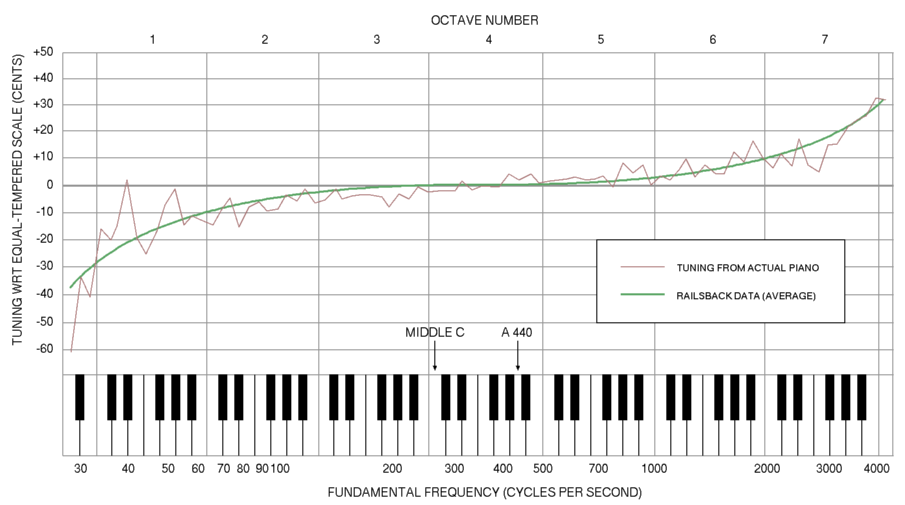
この「対数グラフ(と近しいもの)」が「どう使いやすく、どう使いにくいのか」の感覚的なものについては、この online Spectrum Analyzer を動かしてみればわかるかと。(Logarithmic Frequency Scale? のチェックを付け外してみるといい。)低周波ほど「見やすくなる」一方で、それってのはつまり「低周波だけが妙に拡大されてみえてしまう」ことも意味するのであって、これがわかりやすく感じるかどうかはひとえに「慣れ次第」ってとこだろう。
なお、あげたスクリプトは整理すればそこそこな汎用モジュール目指せる。けどアタシはやんない。本題じゃないし。
2019-01-01 追記:
@きよし(Akiyoshi)/JS1CPW さんのものに基づいた計算をしていたのだけれど、どうもオクターブ No. が一つズレてるんじゃないかという気がしてきた。
ffmpeg の showcqt:
The filter accepts the following options:
…
basefreq
endfreq
fontcolor
…
midi(f)
この説明とワタシ(と Akiyoshi さん)の計算が全然合わないのでなんでだろうと思っていたのだが、同じように WIKIPEDIA: Piano_acoustics にあるこの計算:
とも同様に合わず、そして WIKIPEDIA: Piano_acoustics と ffmpeg の計算は合ってるみたい。で、ワタシの計算をオクターブ番号を一つズラすと完全に合う、具体的には:
1 import math
2
3 #
4 # see details: https://en.wikipedia.org/wiki/MIDI_tuning_standard
5 #
6 _SCALES_L = ["C", "C#/Db", "D", "D#/Eb", "E", "F", "F#/Gb", "G", "G#/Ab", "A", "A#/Bb", "B"]
7
8 def _nn2scale(d):
9 ##return int(d / 12) - 2, _SCALES_L[int(d) % 12]
10 return int(d / 12) - 1, _SCALES_L[int(d) % 12]
11
12 def _nn2freq(d):
13 return math.pow(2, (d - 69) / 12.) * 440
14
15 def _freq2nn(f):
16 return 69 + 12 * math.log(f / 440., 2)
とすると一致する。でよくよく元々の MIDI_tuning_standard を読み返してみると、ここではオクターブ No に対する言及はどこにもされてないのだよねぇ。うーん、何か流儀の違いとかある? いずれにしても ffmpeg と WIKIPEDIA: Piano_acoustics の方に合わせるにはオクターブ番号を最初にワタシがやったヤツから一つズラさないといけないのは確か。
と再び MIDI_tuning_standard をガン見。あ、octave の説明に跳べるな。これは:
\(
\text{Number of octaves} = \log_2\left(\frac{f_2}{f_1}\right)
\)
オクターブというか「オクターブ差」の計算、結局 f1 が何かつー話か…。