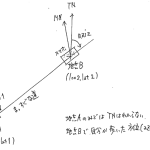
数学的な抽象論としては「周期的な値の平均値(Mean of circular quantities)」ということになるけれど、やりたかったのは「角度の平均」。
どうにも何度もこれ考えてるはずなのに、過去にちゃんと解決した記憶がない。改めて考えてみたら結構ハマった、というハナシ。
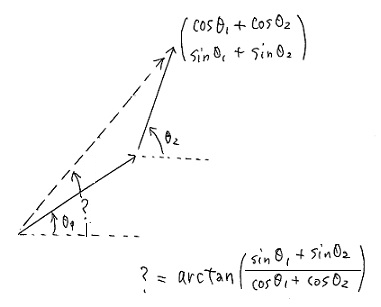
机上で考えたアプローチは至って単純明快:
単位ベクトルのベクトル演算ね。atan は atan2 を使うとして、これの繰り返しなのだから、
\(
\;\;\;\;\bar{\theta} = \mathrm{atan2}\left(\sum_{j=1}^n \sin\theta_j, \sum_{j=1}^n \cos\theta_j\right)
\)
てことでしょう、と。
今ひとつ自信がないので調べ始めてみて混乱。結論としては考え方は間違ってないんだけれど、特異点(?)があるのなぁ…。これは後述するとして、もうひとつ、複素数で計算しても全く同じ:
\(
\;\;\;\;\overline{\mathbf{\rho}}=\displaystyle\frac{1}{N}\sum_{n=1}^N \left(\cos(\theta_n)+i\,\sin(\theta_n)\right)
\\
\;\;\;\;\overline{\theta}=\mathrm{Arg}(\overline{\mathbf{\rho}})
\)
Arg は偏角ね。
どちらの計算についても素直に python 使って書けば、だいたいこんな具合:
1 # -*- coding: utf-8 -*-
2 from math import degrees, radians, cos, sin, atan, atan2
3 import cmath
4 import numpy as np
5
6 # 以下いずれの関数も、a には degrees で [0, 45, 90] のように含まれているとして、
7 # degrees で返す。numpy がないと書けないわけではないが numpy の方が一気に書けて
8 # 読みやすいのでここでは numpy 使っている。
9
10 def mean_of_angle_1(a):
11 y = np.sin(np.radians(a)).sum()
12 x = np.cos(np.radians(a)).sum()
13 return degrees(atan2(y, x))
14
15 def mean_of_angle_2(a):
16 rho = sum(cmath.rect(1, radians(d)) for d in a)
17 rho /= len(a)
18 th = cmath.phase(rho)
19 return degrees(th)
順を追って考える。まず、0度と90度ではどうなる? 絵にすれば分かるとおり、これは45度。上記コードの計算結果もそうなる。0度と135度では67.5度。45度と45度では45度。なのでここまでの計算では普通の算術平均と同じ結果になる。0度と270度ならば、315度か-45度のはずで、上記コードでは-45度を返す。(同じく 270度と270度では-90度。)
じゃぁ、0度と180度、1度と181度、ではどう?
90度と92度だ、と思ってしまったし、事実前者は上のコードでの結果は確かに90度を返す。具体的に…:
1 for i in range(0, 180, 3):
2 a = [i, i+180]
3 r1, r2 = mean_of_angle_1(a), mean_of_angle_2(a)
4 print("%s, %.2f, %.2f" % (a, r1, r2))
この結果に納得出来るだろうか:
1 [0, 180], 90.00, 90.00
2 [3, 183], 90.00, 90.00
3 [6, 186], -90.00, -90.00
4 [9, 189], 90.00, 90.00
5 [12, 192], -56.31, -56.31
6 [15, 195], -90.00, -90.00
7 [18, 198], 135.00, 135.00
8 [21, 201], -90.00, -90.00
9 [24, 204], 0.00, 0.00
10 [27, 207], 90.00, 90.00
11 [30, 210], -56.31, -56.31
12 [33, 213], 0.00, 0.00
13 [36, 216], 90.00, 90.00
14 [39, 219], -63.43, -63.43
15 [42, 222], 0.00, 0.00
16 [45, 225], 180.00, 180.00
17 [48, 228], -45.00, -45.00
18 [51, 231], 135.00, 135.00
19 [54, 234], 135.00, 135.00
20 [57, 237], 0.00, 0.00
21 [60, 240], 146.31, 146.31
22 [63, 243], 180.00, 180.00
23 [66, 246], -45.00, -45.00
24 [69, 249], 161.57, 161.57
25 [72, 252], 180.00, 180.00
26 [75, 255], 0.00, 0.00
27 [78, 258], 180.00, 180.00
28 [81, 261], 135.00, 135.00
29 [84, 264], -48.81, -48.81
30 [87, 267], 180.00, 180.00
31 [90, 270], 180.00, 180.00
32 [93, 273], 0.00, 0.00
33 [96, 276], -168.96, -168.96
34 [99, 279], 180.00, 180.00
35 [102, 282], 53.13, 53.13
36 [105, 285], -168.69, -168.69
37 [108, 288], 180.00, 180.00
38 [111, 291], 0.00, 0.00
39 [114, 294], -156.04, -156.04
40 [117, 297], -116.57, -116.57
41 [120, 300], 18.43, 18.43
42 [123, 303], -153.43, -153.43
43 [126, 306], -135.00, -135.00
44 [129, 309], 45.00, 45.00
45 [132, 312], -143.13, -143.13
46 [135, 315], -135.00, -135.00
47 [138, 318], 71.57, 71.57
48 [141, 321], -126.87, -126.87
49 [144, 324], -90.00, -90.00
50 [147, 327], 71.57, 71.57
51 [150, 330], -123.69, -123.69
52 [153, 333], -90.00, -90.00
53 [156, 336], 51.34, 51.34
54 [159, 339], -111.80, -111.80
55 [162, 342], -90.00, -90.00
56 [165, 345], 71.57, 71.57
57 [168, 348], -101.31, -101.31
58 [171, 351], -90.00, -90.00
59 [174, 354], 90.00, 90.00
60 [177, 357], -90.00, -90.00
冷静に考えるとまず 0度と180度で90度になると思っているのがオカシかったりする。実際に東に一歩行った後で西に一歩戻ったとする。なんで90度? これはどこにも行っていないので、つまり角度が「ない」と言わなければならないのでは?
計算上はこれは atan2 に渡ることになる y, x が誤差で限りなくゼロに近い非ゼロになっていることから起こっている。これが y, x == 0, 0 になっていれば、python なら 0.0、C++11 の std::atan2 では domain error になるがゼロでないので上の結果のような不定値になってしまうようだ。
結局「どこにも行けない角度」→「角度とは言えない」ということで、None なり NaN とするしかないのかなぁと:
1 # -*- coding: utf-8 -*-
2 from math import degrees, radians, cos, sin, atan, atan2
3 import cmath
4 import numpy as np
5
6 # 以下いずれの関数も、a には degrees で [0, 45, 90] のように含まれて
7 # いるとして、degrees で返す。numpy がないと書けないわけではないが
8 # numpy の方が一気に書けて読みやすいのでここでは numpy 使っている。
9
10 def mean_of_angle_1(a):
11 y = np.sin(np.radians(a)).sum()
12 x = np.cos(np.radians(a)).sum()
13 if np.isclose(y, 0) and np.isclose(x, 0):
14 return np.nan # or None
15 return degrees(atan2(y, x))
16
17 def mean_of_angle_2(a):
18 rho = sum(cmath.rect(1, radians(d)) for d in a)
19 if np.isclose(rho, 0):
20 return np.nan # or None
21 rho /= len(a)
22 th = cmath.phase(rho)
23 return degrees(th)
使いにくくはなるけれど…。