うーむ。
matplotlib ネタなのかもなこれは。
とりあえず 一つ前のものよりは「マシ」にしたヤツ:
1 import numpy as np
2 import matplotlib.pyplot as plt
3 import matplotlib.ticker as ticker
4 from tiny_wave_wrapper import WaveReader, WaveWriter
5
6
7 _SCALES_L = ["C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B"]
8
9 def _nn2scale(d):
10 return int(d / 12) - 2, _SCALES_L[int(d) % 12]
11
12 def _nn2freq(d):
13 return np.pow(2, (d - 69) / 12.) * 440
14
15 def _freq2nn(f):
16 return 69 + 12 * np.log2(f / 440.)
17
18 def _nnformat(f, pos):
19 if f > 0:
20 nn = _freq2nn(f)
21 oc1, sc1 = _nn2scale(int(nn))
22 oc2, sc2 = _nn2scale(int(np.ceil(nn)))
23 return r"""%.2f [%s(%d) $\sim$ %s(%d)]""" % (
24 nn, sc1, oc1, sc2, oc2)
25 return ""
26
27
28 if __name__ == '__main__':
29 import argparse
30 parser = argparse.ArgumentParser()
31 parser.add_argument("mode", choices=["show", "pdf"])
32 parser.add_argument("-s", "--step", type=int)
33 parser.add_argument("-u", "--upper_limit_of_view", help="Hz", type=int)
34 parser.add_argument("-l", "--lower_limit_of_view", help="Hz", type=int)
35 parser.add_argument("-c", "--channel", choices=["both", "left", "right"])
36 parser.add_argument("target")
37 args = parser.parse_args()
38
39 with WaveReader(args.target) as fi:
40 nchannels, width, rate, nframes, _, _ = fi.getparams()
41 raw = np.fromstring(fi.readframes(nframes), dtype=np.int16)
42 channels = raw[::2], raw[1::2]
43
44 if args.step:
45 step = args.step
46 else:
47 step = rate // 8
48 fig, ax = plt.subplots()
49 if args.mode == "pdf":
50 fig.set_size_inches(16.53 * 4, 11.69 * 2)
51 for chn in range(len(channels)):
52 if args.channel == "left":
53 if chn == 1:
54 continue
55 ax1 = ax
56 elif args.channel == "right":
57 if chn == 0:
58 continue
59 ax1 = ax
60 else:
61 ax1 = plt.subplot(2, 1, chn + 1)
62 plt.setp(ax1.get_xticklabels(), fontsize=8)
63 plt.setp(ax1.get_yticklabels(), fontsize=8)
64 #
65 F = np.array([])
66 channel = channels[chn]
67 nframes = len(channel)
68 nframes -= (nframes % step) # drop the fraction frames
69 for i in range(0, nframes, step):
70 f = np.abs(np.fft.fft(channel[i:i + step]))
71 f = f / f.max()
72 F = np.vstack((F, f)) if len(F) else f
73
74 freq = np.fft.fftfreq(F.shape[1], 1./rate)
75 X = np.arange(F.shape[0]) / (rate / step) * (2 / width)
76 Y = freq[:len(freq) // 2]
77 Z = F.T[:len(freq) // 2,:]
78 if args.upper_limit_of_view:
79 ind = (Y <= args.upper_limit_of_view)
80 Z = Z[ind, :]
81 Y = Y[ind]
82 if args.lower_limit_of_view:
83 ind = (Y >= args.lower_limit_of_view)
84 Z = Z[ind, :]
85 Y = Y[ind]
86 ax1.contour(X, Y, Z, cmap='jet')
87 ax1.set_ylabel("in Hz")
88 ax1.grid(True)
89
90 ax2 = ax1.twinx()
91 plt.setp(ax2.get_xticklabels(), fontsize=8)
92 plt.setp(ax2.get_yticklabels(), fontsize=8)
93 ax2.contour(X, Y, Z, cmap='jet')
94 ax2.yaxis.set_major_formatter(ticker.FuncFormatter(_nnformat))
95 ax2.set_ylabel("in scale (approx)")
96 ax2.grid(True)
97
98 if args.mode == "pdf":
99 plt.savefig(args.target + ".pdf", bbox_inches="tight")
100 else:
101 plt.tight_layout()
102 plt.show()
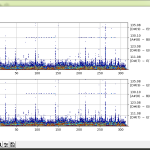
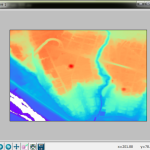
フォントサイズの変更みたいなのはすぐに理解出来るでしょ。抜本的な部分は「クリップ出来るように」と「片方チャンネルだけ見れるように」。ある「電子ピアノ曲の右チャンネルのみの 3000Hz 以下」への適用例:
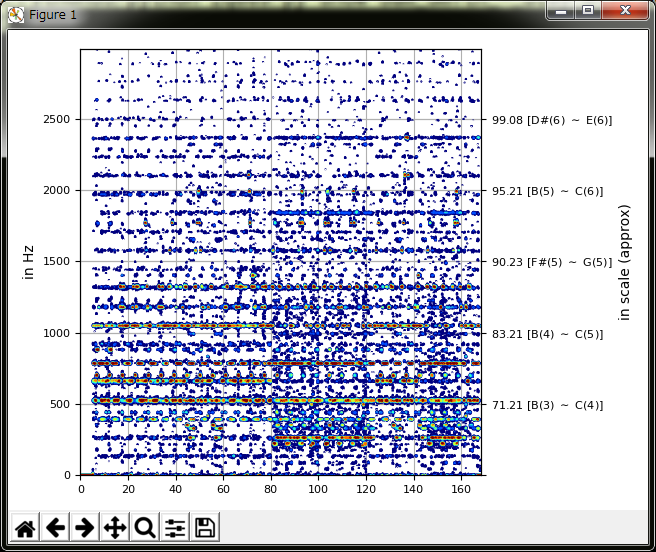
これ「ピアノビギナーズ向け練習動画」だったヤツなので、綺麗に周波数が分解される。
「log2 スケール」なんてのを描ければ期待に近いもの(音階が主役のスケール)になりそうなのだが…。log スケール自体は matplotlib で出来るけれど、無論これは log10 スケール。うーん、ないか? 自力ないとダメかも。