これの続き。
前回のは微妙に悔しかったのである。「Python 本体だけで「Round half away from zero と Round half to even 両方」は出来ないのでプログラム的にやろうとするとちょい面倒」がね。それだけでなくて、いつものようにWikipedia 日本語版とWikipedia 英語版の記述ボリュームがかけ離れてることも気になって。
今回のものについては英語版の方が記述が厚い。いい加減こういう学術的な記述くらいは歩み寄らんけ?
さて。この Wikipedia に書かれてる全部を網羅しようなんてことは思わないけれど、「Rounding to integer – Tie-breaking」のものは全部やってみておこうかなと。「英語版の特典」として、計算式が書かれてるのねぇ:
- Round half up
- \(\lfloor x ~+~ 0.5 \rfloor\)
- Round half down
- \(\lceil x ~-~ 0.5 \rceil\)
- Round half towards zero
- \({\rm sgn}(x) \lceil ~ \left| x \right| ~-~ 0.5 \rceil\)
- Round half away from zero
- \({\rm sgn}(x) \lfloor ~ \left| x \right| ~+~ 0.5 \rfloor\)
half to even と half to odd が文章だけで書かれていて一撃の式が書かれていないようにみえて、実はそうでもない。寝ながら思いついたんだけれど、たぶんこれでいい(と思う):
- Round half to even
- 整数部が奇数ならば Round half away from zero
- 整数部が偶数ならば Round half towards zero
- Round half to odd
- 整数部が奇数ならば Round half towards zero
- 整数部が偶数ならば Round half away from zero
というわけで:
1 from math import floor, ceil, copysign, modf
2
3
4 #
5 # DON'T USE THESE FOR PRODUCTION CODES!!
6 # THESE ARE JUST FOR STUDIES.
7 #
8 def round_half_up(x):
9 """
10 Round half up. (\lfloor x ~+~ 0.5 \rfloor)
11
12 >>> f_ = round_half_up
13 >>> l_ = (4.6, 4.5, 4.4, 3.6, 3.5, 3.4, 0,
14 ... -3.4, -3.5, -3.6, -4.4, -4.5, -4.6)
15 >>> [int(f_(v)) for v in l_]
16 [5, 5, 4, 4, 4, 3, 0, -3, -3, -4, -4, -4, -5]
17 """
18 return floor(x + 0.5)
19
20
21 def round_half_down(x):
22 """
23 Round half down. (\lceil x ~-~ 0.5 \rceil)
24
25 >>> f_ = round_half_down
26 >>> l_ = (4.6, 4.5, 4.4, 3.6, 3.5, 3.4, 0,
27 ... -3.4, -3.5, -3.6, -4.4, -4.5, -4.6)
28 >>> [int(f_(v)) for v in l_]
29 [5, 4, 4, 4, 3, 3, 0, -3, -4, -4, -4, -5, -5]
30 """
31 return ceil(x - 0.5)
32
33
34 def round_half_towards_zero(x):
35 """
36 Round half towards zero.
37 ({\rm sgn}(x) \lceil \left| x \right| ~-~ 0.5 \rceil)
38
39 >>> f_ = round_half_towards_zero
40 >>> l_ = (4.6, 4.5, 4.4, 3.6, 3.5, 3.4, 0,
41 ... -3.4, -3.5, -3.6, -4.4, -4.5, -4.6)
42 >>> [int(f_(v)) for v in l_]
43 [5, 4, 4, 4, 3, 3, 0, -3, -3, -4, -4, -4, -5]
44 """
45 return copysign(ceil(abs(x) - 0.5), x)
46
47
48 def round_half_away_from_zero(x):
49 """
50 Round half away from zero.
51 ({\rm sgn}(x) \lfloor \left| x \right| ~+~ 0.5 \rfloor)
52
53 same as Py2's round(x, 0).
54
55 >>> f_ = round_half_away_from_zero
56 >>> l_ = (4.6, 4.5, 4.4, 3.6, 3.5, 3.4, 0,
57 ... -3.4, -3.5, -3.6, -4.4, -4.5, -4.6)
58 >>> [int(f_(v)) for v in l_]
59 [5, 5, 4, 4, 4, 3, 0, -3, -4, -4, -4, -5, -5]
60 >>> import sysconfig
61 >>> if sysconfig.get_python_version()[0] == '2':
62 ... assert [int(f_(v)) for v in l_] == [int(round(v)) for v in l_]
63 """
64 return copysign(floor(abs(x) + 0.5), x)
65
66
67 def round_half_to_even(x):
68 """
69 Round half to even.
70
71 same as Py3's round(x, 0).
72
73 >>> f_ = round_half_to_even
74 >>> l_ = (4.6, 4.5, 4.4, 3.6, 3.5, 3.4, 0,
75 ... -3.4, -3.5, -3.6, -4.4, -4.5, -4.6)
76 >>> [int(f_(v)) for v in l_]
77 [5, 4, 4, 4, 4, 3, 0, -3, -4, -4, -4, -4, -5]
78 >>> import sysconfig
79 >>> if sysconfig.get_python_version()[0] == '3':
80 ... assert [int(f_(v)) for v in l_] == [int(round(v)) for v in l_]
81 """
82 frac, intp = modf(x)
83 if intp % 2 != 0:
84 return round_half_away_from_zero(x)
85 else:
86 return round_half_towards_zero(x)
87
88
89 def round_half_to_odd(x):
90 """
91 Round half to odd.
92
93 >>> f_ = round_half_to_odd
94 >>> l_ = (4.6, 4.5, 4.4, 3.6, 3.5, 3.4, 0,
95 ... -3.4, -3.5, -3.6, -4.4, -4.5, -4.6)
96 >>> [int(f_(v)) for v in l_]
97 [5, 5, 4, 4, 3, 3, 0, -3, -3, -4, -4, -5, -5]
98 >>> g_ = round_half_to_even
99 >>> [f_(v) - g_(v) for v in l_]
100 [0.0, 1.0, 0.0, 0.0, -1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, -1.0, 0.0]
101 """
102 frac, intp = modf(x)
103 if intp % 2 == 0:
104 return round_half_away_from_zero(x)
105 else:
106 return round_half_towards_zero(x)
107
108
109 if __name__ == '__main__':
110 import doctest
111 doctest.testmod()
注意。この掲載コードが正しい正しくないに関係なく、これを「算数の理解のため」以外の目的には使わないでね。つまり、製品コードで使うのはやらん方がいいと思う。機能面の制約(本物の round にある digits がないとか)のこともあるし、桁溢れ時の振る舞いであるとか、戻り値の型であるとか、とにかくそういった一切合財を真面目にやってやしないんだから。当然組み込みでないわけだから「超遅い」し。なお、たとえば「CPython 2.7 で half to even の(正しい) round を使いたい」ということなら、Python 3.x の Objects/floatobject.c、Objects/longobject.c から関係する部分引っこ抜いて移植するくらしか今のところ手はない気がする。
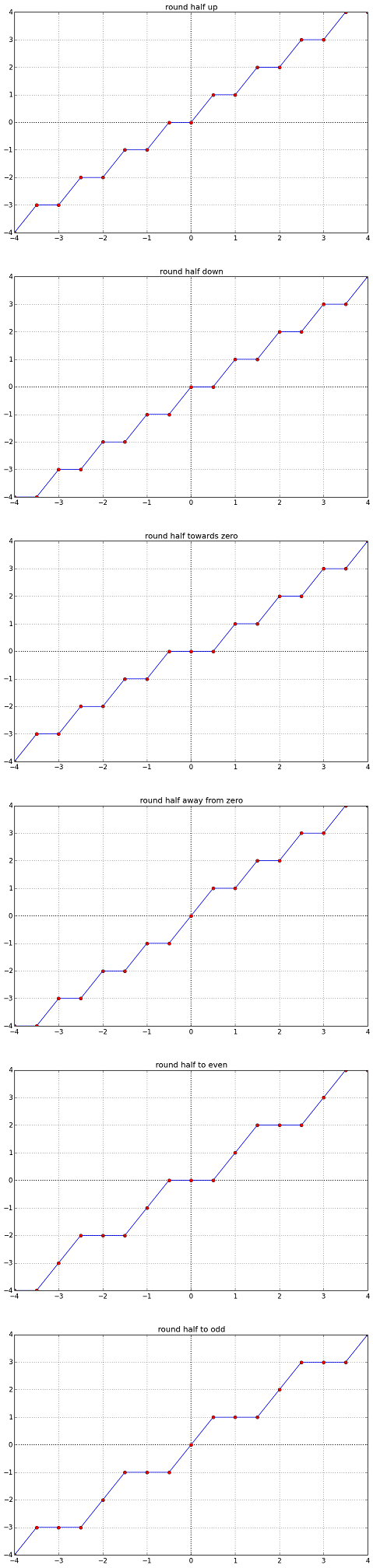
さて。前回可視化したのと似たセンスで絵にしてみる:
1 import numpy as np
2 import matplotlib.pyplot as plt
3 from round_int import (
4 round_half_up,
5 round_half_down,
6 round_half_towards_zero,
7 round_half_away_from_zero,
8 round_half_to_even,
9 round_half_to_odd)
10
11 p = (
12 (round_half_up, "round half up"),
13 (round_half_down, "round half down"),
14 (round_half_towards_zero, "round half towards zero"),
15 (round_half_away_from_zero, "round half away from zero"),
16 (round_half_to_even, "round half to even"),
17 (round_half_to_odd, "round half to odd"),
18 )
19
20 t = np.linspace(-4, 4, 8 * 2 + 1)
21
22 fig, axes = plt.subplots(nrows=len(p))
23 fig.set_size_inches(11.69, 16.53 * 3)
24
25 for i, ax in enumerate(axes):
26 ax.grid(True)
27 ax.axhline(linewidth=1.5, color="black", linestyle="dotted")
28 ax.axvline(linewidth=1.5, color="black", linestyle="dotted")
29 v = [p[i][0](x) for x in t]
30 ax.plot(t, v)
31 ax.plot(t, v, "or")
32 ax.set_title(p[i][1])
33
34 plt.savefig("round.png", bbox_inches="tight")
まぁ…、こんな絵にしたからといって「劇的に」わかりやすくなるもんでもないけどね。(でもまぁ、原点を中心にシンメトリかどうかを知るのには役には立つとは思う。)