(4)からの続き。
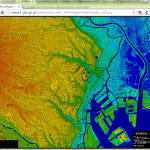
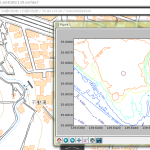
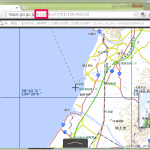
「富士山が切ないことになるに違いない」、つまり広域の扱いの事始め。とりあえず富士山を扱うのに東京・神奈川だけでは足りないので、静岡と山梨も全部ダウンロード・変換しておいた。の上で:
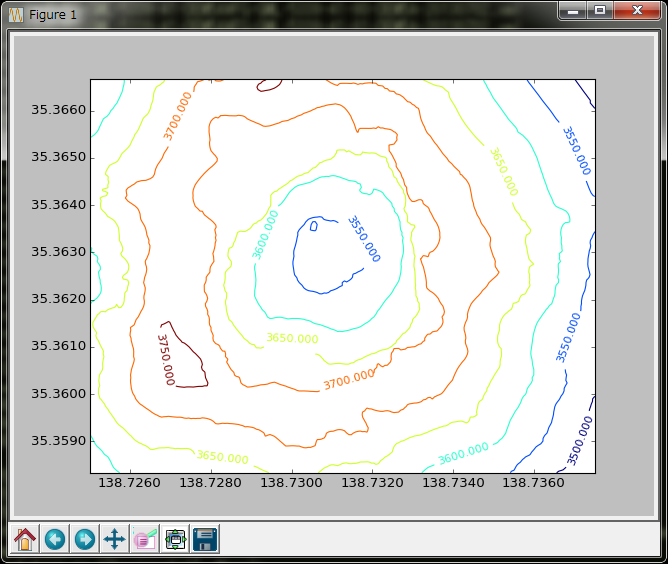
あらまぁ、びっくり。丁度山頂が中心に来ちゃうのか。切なさが伝わらんね、これでは。
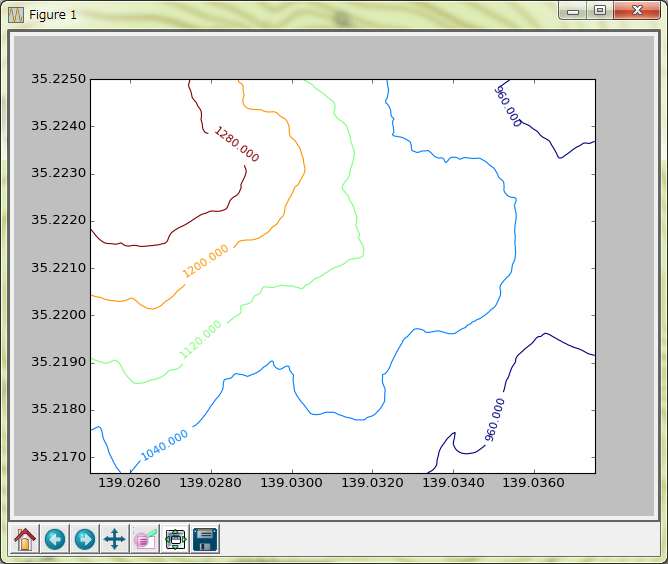
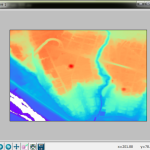
箱根駒ケ岳が丁度よい切なさでしたわ:
左上(北西)部分が駒ケ岳山頂へ向かう傾斜、ですよ。これをお題にしますか、ひとまず。うー、静岡・山梨いらんかったな。
さて。今回の本題は「広域」、プログラミング目線で言えば「セル結合」なわけなんだけれど、そのために必要な部品化の前に、ちょっと整理しとかないと後がツラい。まずこうしとく:
1 # -*- coding: utf-8 -*-
2 import pickle
3 import numpy as np
4
5
6 def _calc_pos0(lon_or_lat, lseg):
7 a = (lon_or_lat % 100) / lseg
8 b = (a - int(a)) / (1 / 8.)
9 c = (b / (1 / 10.)) % 10
10 return (
11 int(a),
12 int(b),
13 int(c),
14 round((int(a) + int(b) / 8. + int(c) / 8. / 10.) * lseg, 9),
15 round((int(a) + int(b) / 8. + (int(c) + 1) / 8. / 10.) * lseg, 9))
16
17
18 def _calc_from_latlon(lat, lon):
19 _fromlat = _calc_pos0(lat, 2/3.)
20 _fromlon = _calc_pos0(lon, 1.)
21 return (
22 "__converted/{}{}-{}{}/{}{}".format(
23 _fromlat[0], _fromlon[0],
24 _fromlat[1], _fromlon[1],
25 _fromlat[2], _fromlon[2]),
26 (_fromlat[3], _fromlon[3] + 100),
27 (_fromlat[4], _fromlon[4] + 100))
28
29
30 lat, lon = 35.224167, 139.025373 # 箱根駒ケ岳
31 base, lc, uc = _calc_from_latlon(lat, lon)
32
33 _m = pickle.load(open(base + ".meta", "rb"))
34 _raw = pickle.load(open(base + ".data", "rb"))
35
36 elevs = np.zeros(_m["shape"][1] * _m["shape"][0])
37 elevs[_m["st"]:len(_raw) + _m["st"]] = _raw
38 elevs = elevs.reshape((_m["shape"][0], _m["shape"][1]))
39 elevs = np.flipud(elevs)
40 print(elevs)
41
42 #
43 import matplotlib
44 import matplotlib.cm as cm
45 import matplotlib.pyplot as plt
46 from matplotlib.ticker import FormatStrFormatter
47
48 fig, ax = plt.subplots()
49 ax.xaxis.set_major_formatter(FormatStrFormatter('%.4f'))
50 ax.yaxis.set_major_formatter(FormatStrFormatter('%.4f'))
51
52 X = np.linspace(lc[1], uc[1], elevs.shape[1])
53 Y = np.linspace(lc[0], uc[0], elevs.shape[0])
54 CS = plt.contour(X, Y, elevs)
55 plt.clabel(CS, inline=1, fontsize=10)
56 plt.show()
簡単にいえばデータの局所化、細かく言えば「緯度経度から計算で求まるものなどは都度計算することで、冗長データをなくす」てこと。これによって、一つのセル((もとの)xml一個)読み出し全体を関数に出来るはずだ、というわけね。興味があるひとは前回のと比較してみて。
ここまでくれば「部品化」は容易い:
1 # -*- coding: utf-8 -*-
2 import pickle
3 import numpy as np
4
5
6 def _calc_pos0(lon_or_lat, lseg):
7 a = (lon_or_lat % 100) / lseg
8 b = (a - int(a)) / (1 / 8.)
9 c = (b / (1 / 10.)) % 10
10 return (
11 int(a),
12 int(b),
13 int(c),
14 round((int(a) + int(b) / 8. + int(c) / 8. / 10.) * lseg, 9),
15 round((int(a) + int(b) / 8. + (int(c) + 1) / 8. / 10.) * lseg, 9))
16
17
18 def _calc_from_latlon(lat, lon):
19 _fromlat = _calc_pos0(lat, 2/3.)
20 _fromlon = _calc_pos0(lon, 1.)
21 return (
22 "__converted/{}{}-{}{}/{}{}".format(
23 _fromlat[0], _fromlon[0],
24 _fromlat[1], _fromlon[1],
25 _fromlat[2], _fromlon[2]),
26 (_fromlat[3], _fromlon[3] + 100),
27 (_fromlat[4], _fromlon[4] + 100))
28
29
30 def load(lat, lon):
31 base, lc, uc = _calc_from_latlon(lat, lon)
32
33 _m = pickle.load(open(base + ".meta", "rb"))
34 _raw = pickle.load(open(base + ".data", "rb"))
35
36 elevs = np.zeros(_m["shape"][1] * _m["shape"][0])
37 elevs[_m["st"]:len(_raw) + _m["st"]] = _raw
38 elevs = elevs.reshape((_m["shape"][0], _m["shape"][1]))
39 elevs = np.flipud(elevs)
40 return elevs, lc, uc
のでメインはこうなる:
1 # -*- coding: utf-8 -*-
2 import numpy as np
3 import converted_loader
4
5
6 lat, lon = 35.224167, 139.025373 # 箱根駒ケ岳
7 elevs, lc, uc = converted_loader.load(lat, lon)
8
9 #
10 import matplotlib
11 import matplotlib.cm as cm
12 import matplotlib.pyplot as plt
13 from matplotlib.ticker import FormatStrFormatter
14
15 fig, ax = plt.subplots()
16 ax.xaxis.set_major_formatter(FormatStrFormatter('%.4f'))
17 ax.yaxis.set_major_formatter(FormatStrFormatter('%.4f'))
18
19 X = np.linspace(lc[1], uc[1], elevs.shape[1])
20 Y = np.linspace(lc[0], uc[0], elevs.shape[0])
21 CS = plt.contour(X, Y, elevs)
22 plt.clabel(CS, inline=1, fontsize=10)
23 plt.show()
ようやく本題に入っていこう。まずは西方向が欲しい。左隣(西)のセルを持ってきて結合してみる:
1 # -*- coding: utf-8 -*-
2 import numpy as np
3 import converted_loader
4
5
6 lat, lon = 35.224167, 139.025373 # 箱根駒ケ岳
7 elevs1, lc1, uc1 = converted_loader.load(lat, lon)
8 elevs2, lc2, uc2 = converted_loader.load(lat, lon - 1 / 8. / 10.)
9 elevs = np.hstack((elevs2, elevs1))
10 lc = (min(lc1[0], lc2[0]), min(lc1[1], lc2[1]))
11 uc = (max(uc1[0], uc2[0]), max(uc1[1], uc2[1]))
12
13
14 #
15 import matplotlib
16 import matplotlib.cm as cm
17 import matplotlib.pyplot as plt
18 from matplotlib.ticker import FormatStrFormatter
19
20 fig, ax = plt.subplots()
21 ax.xaxis.set_major_formatter(FormatStrFormatter('%.4f'))
22 ax.yaxis.set_major_formatter(FormatStrFormatter('%.4f'))
23
24 X = np.linspace(lc[1], uc[1], elevs.shape[1])
25 Y = np.linspace(lc[0], uc[0], elevs.shape[0])
26 CS = plt.contour(X, Y, elevs)
27 plt.clabel(CS, inline=1, fontsize=10)
28 plt.show()
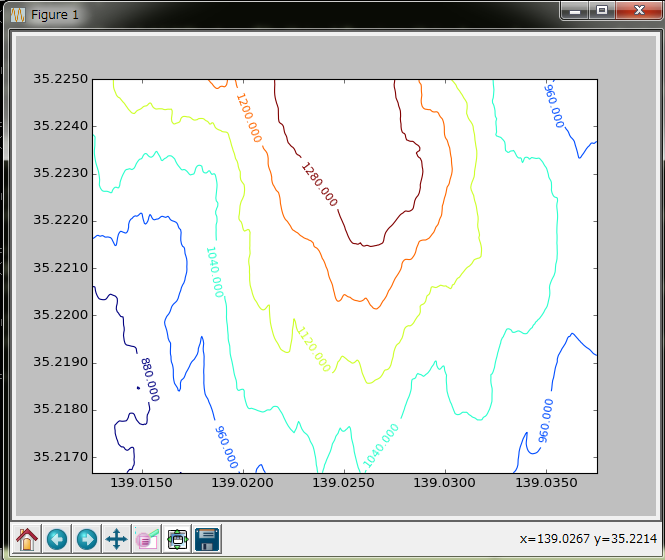
横方向の行列の結合は hstack で簡単に出来る。X, Y は、upper corner、lower corner の単体セルとしてのではなく全体から作れる。結果はこう:
アスペクト比が狂ってるのは気にしない。詳しい人なら最初からアスペクト比がおかしいことは気付いていたはず。緯度経度は1度あたりの距離は場所によっても異なるし矩形でもない(緯度一度の距離と経度1度の距離は全然違う)。これは最後の最後にやるつもりなので、今はこんなでも全く気にしない。
で、今度は上(北)を結合する:
1 # -*- coding: utf-8 -*-
2 import numpy as np
3 import converted_loader
4
5
6 lat, lon = 35.224167, 139.025373 # 箱根駒ケ岳
7 elevs1, lc1, uc1 = converted_loader.load(lat, lon)
8 elevs2, lc2, uc2 = converted_loader.load(lat, lon - 1 / 8. / 10.)
9 elevs3, lc3, uc3 = converted_loader.load(
10 lat + 2./3 / 8 / 10, lon)
11 elevs4, lc4, uc4 = converted_loader.load(
12 lat + 2./3 / 8 / 10, lon - 1 / 8. / 10.)
13 elevs = np.vstack((
14 np.hstack((elevs2, elevs1)),
15 np.hstack((elevs4, elevs3))
16 ))
17 lc = (
18 min(lc1[0], lc2[0], lc3[0], lc4[0]),
19 min(lc1[1], lc2[1], lc3[1], lc4[1]))
20 uc = (
21 max(uc1[0], uc2[0], uc3[0], uc4[0]),
22 max(uc1[1], uc2[1], uc3[1], uc4[1]))
23
24
25 #
26 import matplotlib
27 import matplotlib.cm as cm
28 import matplotlib.pyplot as plt
29 from matplotlib.ticker import FormatStrFormatter
30
31 fig, ax = plt.subplots()
32 ax.xaxis.set_major_formatter(FormatStrFormatter('%.4f'))
33 ax.yaxis.set_major_formatter(FormatStrFormatter('%.4f'))
34
35 X = np.linspace(lc[1], uc[1], elevs.shape[1])
36 Y = np.linspace(lc[0], uc[0], elevs.shape[0])
37 CS = plt.contour(X, Y, elevs)
38 plt.clabel(CS, inline=1, fontsize=10)
39 plt.show()
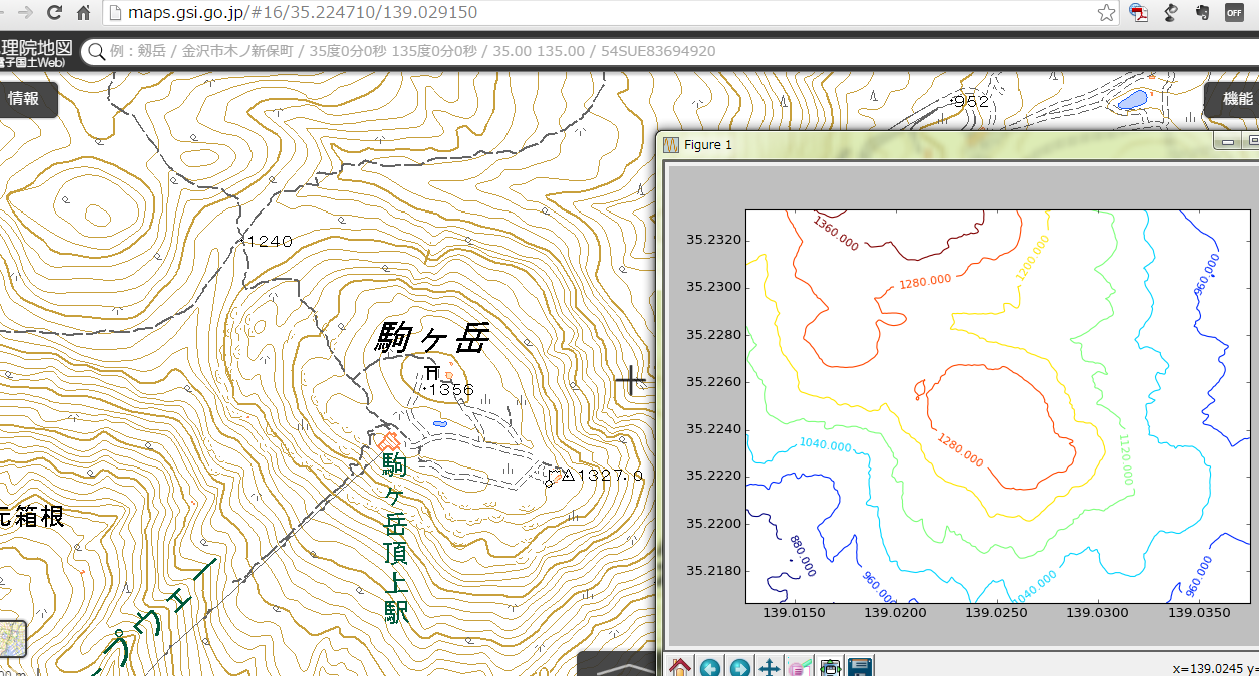
行列の縦方向の結合は vstack。こうなった:
良いね。
あとはこの隣接セルの探索と結合をもっと汎用的に書く必要があるけど、ちょっと今回長くなってしまったので、これは次回ということで。かなりの広域を扱いたくなるとデータサイズが問題になってくるので、データの丸めとかもやってかないといけないんだけど、これもいずれ。