n乗根の話? いや、そっちじゃなくて。

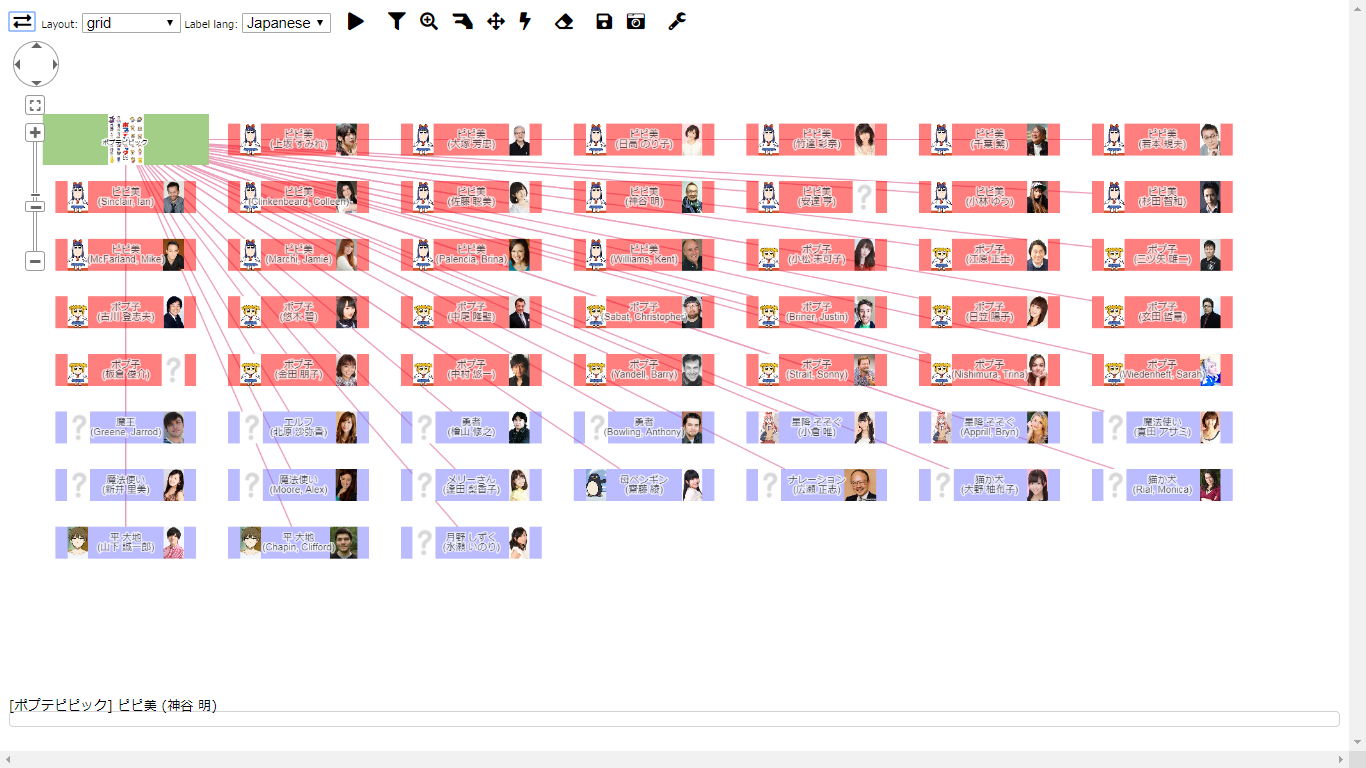
実は Cytoscape.js ネタからのニーズ。grid レイアウトがね、デフォルトが賢くなくて:

いやいや、もっと上下の方を有効活用してくれよ、て誰だって思う。これは一応 rows, cols でコントロールは出来るのだけど、なんかねぇ、賢く自動でやるからにはもうちっと頑張って欲しい。

でワタシのヤツの場合はシンプルにノード数の二乗根でまぁ十分で:

 1 // initialize cy
 2 var cy = window.cy = cytoscape({
 3     container: document.getElementById('cy'),
 4     // ...
 5 });    
 6 var num = ...; // ノード数
 7 var layopt = {
 8     name: "grid",
 9     avoidOverlap: true,
10     fit: true,
11     cols: parseInt(Math.sqrt(num)),  // ノード数の二乗根
12 };
13 cy.elements().makeLayout(layopt).run();

みたいにすれば:

というわけでいい感じ、なわけだけれど。

ただ、「正方(square)」で配置したいとは限らんのよねぇ、と考えるとすればどうなるか、という話。

なんかすげー基礎的なことのように思えるのだけれど、なんかワタシはお仕事なり遊びなりどっちでもいいけれど、この計算の必要性を感じた記憶が全くない。ただ高校生レベルの数学として習った記憶はないし、大学教養レベルでも同じく、学部時代・大学院時代でさえ、この算数の記憶が全くない。

ちょっと探っただけでこの演算が rectangle root なのだということがわかり、そして:

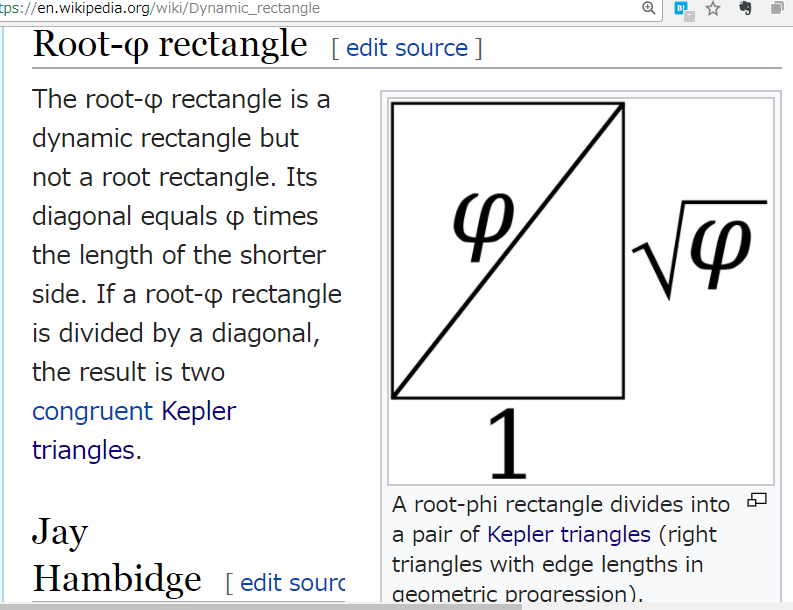
うーんっと、どう考えればいいか。たぶん(cols を c 、nodes を n として) \(c^2 \times \sqrt{\varphi} \le n\)　の最大の c を求める、てことになるのかな? \(\varphi\)は単に「縦横比」(の二乗)そのものだと思えばいい(すなわち実際の適用時は定数)のでいいんだけど、うーん、一回の計算だけでは行けんのだね。となれば、最初に「およそのあたりをつける」ことから始めると良さそうだが、そんなんすぐに決まるかね?

まぁいいか、以上、皮算用終わり。「一撃では計算出来ないので少しだけ大変」てことだわね。合ってる?

05:20追記:
「の最大」なんて考えなくていいよね、よく考えたら。だって二乗根求めるときだって、結果を整数に丸めてるだけだもん。なので、cols を c 、nodes を n として
\(
c \;=\; \sqrt{\frac{n}{\sqrt{\varphi}}}
\)
で十分だ、てことだ。今考えてるヤツの場合は\(\sqrt{\varphi}\)がアスペクト比そのものなので、これを例えばαとすれば:
\(
c \;=\; \sqrt{\frac{n}{\alpha}}
\)
てだけね。なんだよ簡単じゃねーか。なんならこれ、中学生でも出来る計算ね。