Python 2.6 と 2.7 での「整数かどうか」チェック

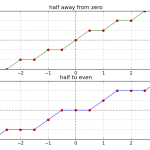
What’s old てて良かった話、アナザーストーリー。

Python の欠陥ネタを大喜びで書く人なんていくらでもいて、人を集められるからいいんだろうね、「落とし穴だら、死ねやヲラ」⇒「んな知ったこと言うなや、知らんのなら知らんと言えや」の連鎖がままあるのだいね。

なんだらう、「これぞ Python の落とし穴だ!」への反論な「いやいやそんなの Python 知らんからやろ、そんなこと言うならワシが書いたるわい、これがほんとの落とし穴だ」なネタのとこ読んでてさ、なんとも苦々しいのだわいね。何かつうと「数値型の設計」についての話。「int と long が別なんてどーかしてるぜ!」てわけだ。

実際その通りなんだけど、そんなの随分前、10年以上前から Python デベロッパの間でずっと議論されてたことだし、Python 3 で解消したんだから何を今更言ってんの、とも思うし、「int と long が別なんてどーかしてるぜ!」という本題はともかく、件のサイトが挙げてる例示がまったく腑に落ちないとこもあってな、なんだかなぁ、と思っておった。

「件のサイトが挙げてる例示」が教育上よろしくないのが、「isinstance で型をチェック出来るべし/すべし」があたかも常識であるかのように書かれていることだ。違うであろう? そこで例にされているような、「相手にする何かが type sensitive なのでやむなく」のために特別に許されるようなものである、isinstance での明示的な型テストなんぞは。

当たり前のことだが「ダメと言われたって必要なときは必要」だから isinstance は存在している。けれども isinstance が日常使いになってるなら、考えを改めたほうがいいだろう。そんなもんは限られたディスパッチャにかき集めるべきだ。あちこちにバラまくもんじゃない。

というようなことをずっと考えていたんだけれども、とはいえ「必要なときは必要」な「そのとき」の一つの特殊例として、「int と long が別物であること」が問題なのは、これは確かなのね。そしてあたしゃずっと、その解は

1 isinstance(n, (int, long))

しかないんだと思い込んでいた。これの何がイヤだって、Python 3 でこれはダメなことだ。Python 3 には「整数、長整数」なんて区別はないんであって、なので long なんて型はない。

ここんとこの「What’s old 翻訳祭り」で、はじめて numbers の価値を知った。存在は知ってたけど使おうと思ったことがなかったが、翻訳で真剣に読んでるうちに理解できてきた。

あ、そうか、この ABC と組み合わせれば「Python 2 系と 3 でどっちでも使える整数かどうかチェック」が書けそうだな、と。やってみた：

Integral はぶっちゃけて言えばビットシフト演算出来るもの、ゆえ、整数が該当。

 1 Python 2.7.9 (default, Dec 10 2014, 12:28:03) [MSC v.1500 64 bit (AMD64)] on win32
 2 Type "help", "copyright", "credits" or "license" for more information.
 3 >>> import numbers
 4 >>> import fractions
 5 >>> import decimal
 6 >>> 
 7 >>> isinstance(10.0, (numbers.Integral))
 8 False
 9 >>> isinstance(complex(1, 2), (numbers.Integral))
10 False
11 >>> isinstance(fractions.Fraction(2, 3), (numbers.Integral))
12 False
13 >>> isinstance(decimal.Decimal(10), (numbers.Integral))
14 False
15 >>> isinstance(decimal.Decimal(10.3), (numbers.Integral))
16 False
17 >>> isinstance("abc", (numbers.Integral))
18 False
19 >>> isinstance(u"abc", (numbers.Integral))
20 False
21 >>> isinstance(type(1), (numbers.Integral))
22 False
23 >>> isinstance([1,], (numbers.Integral))
24 False
25 >>> isinstance((1,), (numbers.Integral))
26 False
27 >>> isinstance((i for i in range(10)), (numbers.Integral))
28 False
29 >>> isinstance(range(10), (numbers.Integral))
30 False
31 >>> 
32 >>> isinstance(10, (numbers.Integral))
33 True
34 >>> isinstance(2<<40, (numbers.Integral))
35 True

うん、よかね。はぁ、ちょっとスッキリした。

ちなみに上のチェックは「int もしくは long」をチェックしたいんであって、「整数かどうか」とは違うのは見ての通り。本当の意味での「整数かどうか」を「型のみ」から知るのは無理があって、Decimal でも Fraction でも端数部がないかをテストする必要があるし、「1.0 は整数だ」と言い張りたければそれも同じ話。まぁ何をしたいかによるわいね。

ほいで最後にも一回念押ししとくよ。「型の明示的なテストは本当に必要なの?」は必ず自問してください。大抵それに拠らずに書けるはずで、これが本当に必要になる場所は結構限られてて、「型に繊細な(主として非 Python) API を呼び出す必要がある場合」でないケースで isinstance 使うのは大抵(8 割以上)間違ってます。

ところで numbers なんだけど、「価値はある」ことは認めつつも、このデザインはちょっと、というかかなり中途半端だと思う。

数学的抽象としての「複素数 ← 実数 ← 有理数 ← 整数」という派生関係はたぶん正しい。「実数は虚数部がゼロの虚数の特殊ケース」「有理数は分数で表現可能な実数の特殊ケース」「整数は分子が分母で割り切れる有理数の特殊ケース」なので、まったくもって包含関係は正しい。

けれど、「適用可能な演算の集合」となると、ちょっと違和感がある。例えば floor が「実数でのみ使える」として「Real」での追加演算としているんだけど、抽象論としてそれは正しいのか? 複素数の「床」は、定義しようと思えば出来るんではないかね。なんかちょっと「実装が許していないから」というのと抽象論が混同してデザインされてやしないか。

ワタシは数学やさんではないので厳密な議論はわからないけれど、「複素数が世界だ」という集合の包含関係から考えればさ、最も基底の複素数に演算が全部いないとヘンなんじゃないのか、って思っちゃうんだけど。つまり「定義しさえすればそれが世界」なんでは。数学の抽象論てそういうもんでしょ。(ちなみに NumPy でも複素数に floor 使えないのは一緒。)

あとこれはもう Python の宿命であってきゃー ruby すてきぃ、なゾーンだけどさ、今更だけどこれはやっぱちょっとやぁねぇ：

 1 >>> a = 3.5
 2 >>> a.conjugate()
 3 3.5
 4 >>> 3.5.conjugate()
 5 3.5
 6 >>> 3.conjugate()
 7   File "<stdin>", line 1
 8     3.conjugate()
 9               ^
10 SyntaxError: invalid syntax