本題ではあるけれどただの整理、とも言える、「サイズ縮小をよきにはからう」。
(9)でサイズ縮小出来るようにしたのはいいんだけれど、色んな領域で試行錯誤したりとかを繰り返すにつれ、この縮小率の微調整がだんだん手間に感じてきた。というか「縮小率での試行錯誤はしたくない」。何より「残念」なのは、5mメッシュを最大限に活かせるような小領域に対して、縮小を外し忘れてしまいがちな点。
公約数のリストの求め方がわかったことだし、ある程度自動で計算するようにしてみますか、と。
もうイキナリ答え:
1 # -*- coding: utf-8 -*-
2 import os
3 import logging
4 try:
5 # for CPython 2.7
6 import cPickle as pickle
7 except ImportError:
8 # Python 3.x or not CPython
9 import pickle
10 import numpy as np
11 import scipy.ndimage as ndimage
12
13
14 _logger = logging.getLogger(__name__)
15
16
17 def _calc_pos0(lon_or_lat, lseg):
18 a = (lon_or_lat % 100) / lseg
19 b = (a - int(a)) / (1 / 8.)
20 c = (b / (1 / 10.)) % 10
21 return (
22 int(a),
23 int(b),
24 int(c),
25 round((int(a) + int(b) / 8. + int(c) / 8. / 10.) * lseg, 9),
26 round((int(a) + int(b) / 8. + (int(c) + 1) / 8. / 10.) * lseg, 9))
27
28
29 def _calc_from_latlon(lat, lon):
30 _fromlat = _calc_pos0(lat, 2/3.)
31 _fromlon = _calc_pos0(lon, 1.)
32 return (
33 "{}{}/{}{}/{}{}".format(
34 _fromlat[0], _fromlon[0],
35 _fromlat[1], _fromlon[1],
36 _fromlat[2], _fromlon[2]),
37 (_fromlat[3], _fromlon[3] + 100),
38 (_fromlat[4], _fromlon[4] + 100))
39
40
41 _shape = (150, 225)
42
43
44 def _load0(fn):
45 with open(fn, "rb") as fi:
46 _d = pickle.load(fi)
47 _st = _d["startPoint"]
48 _raw = _d["elevations"]
49 elevs = np.full((_shape[1] * _shape[0], ), np.nan)
50 elevs[_st:len(_raw) + _st] = _raw
51 elevs = elevs.reshape((_shape[0], _shape[1]))
52 return np.flipud(elevs)
53
54
55 def load(lat, lon, convert_fun=None, use_dem10=True):
56 base, lc, uc = _calc_from_latlon(lat, lon)
57
58 dem05fn = "__converted/DEM05/" + base + ".data"
59 dem10fn = "__converted/DEM10/" + base + ".data"
60
61 elevs1, elevs2 = None, None
62
63 if use_dem10 and os.path.exists(dem10fn):
64 elevs1 = _load0(dem10fn)
65 if convert_fun:
66 elevs1 = convert_fun(elevs1)
67
68 if os.path.exists(dem05fn):
69 elevs2 = _load0(dem05fn)
70 if convert_fun:
71 elevs2 = convert_fun(elevs2)
72
73 if elevs1 is None:
74 if elevs2 is None:
75 elevs = np.full((_shape[0], _shape[1]), np.nan)
76 if convert_fun:
77 elevs = convert_fun(elevs)
78 _logger.info("data was not found: {}".format(base))
79 else:
80 elevs = elevs2
81 _logger.info("DEM5: {}".format(base))
82 else:
83 elevs = elevs1
84 if elevs2 is not None:
85 notnan = (np.isnan(elevs2) == False)
86 elevs[notnan] = elevs2[notnan]
87 _logger.info("DEM5 + DEM10: {}".format(base))
88 else:
89 _logger.info("DEM10: {}".format(base))
90
91 return elevs, lc, uc
92
93
94 def _calc_cellnums(lc_lat, lc_lon, uc_lat, uc_lon):
95 #
96 ydis = (2. / 3 / 8 / 10)
97 xdis = (1. / 8 / 10)
98
99 # adjust startpoint to center of mesh
100 # (for special boundary case.)
101 lc_lat = int(lc_lat / ydis) * ydis + ydis / 2.
102 lc_lon = int(lc_lon / xdis) * xdis + xdis / 2.
103
104 ycells = int(np.ceil(uc_lat / ydis) - np.floor(lc_lat / ydis))
105 xcells = int(np.ceil(uc_lon / xdis) - np.floor(lc_lon / xdis))
106
107 return xdis, ydis, xcells, ycells, lc_lat, lc_lon
108
109 def _load_range0(lc_lat, lc_lon, uc_lat, uc_lon, convert_fun=None, use_dem10=True):
110 #
111 def _stfun(fun, left, right):
112 if left is None:
113 return right
114 return fun((left, right))
115 #
116 xdis, ydis, xcells, ycells, lc_lat, lc_lon = \
117 _calc_cellnums(lc_lat, lc_lon, uc_lat, uc_lon)
118
119 result, lc, uc = None, None, None
120 #
121 for i in range(ycells):
122 tmp = None
123 for j in range(xcells):
124 e, lc_tmp, uc_tmp = load(
125 lc_lat + ydis * i,
126 lc_lon + xdis * j,
127 convert_fun, use_dem10)
128 #
129 if not lc:
130 lc = lc_tmp
131 uc = uc_tmp
132 #
133 tmp = _stfun(np.hstack, tmp, e)
134 #
135 result = _stfun(np.vstack, result, tmp)
136 #
137 return result, lc, uc
138
139
140 def _common_divisors(a, b):
141 while b:
142 a, b = b, a % b
143 return [d for d in range(2, a // 2 + 1) if a % d == 0] + [a]
144
145
146 class _DownSizer(object):
147 def __init__(self, level):
148 self.level = level
149
150 def __call__(self, d):
151 if self.level == 1:
152 return d
153 return ndimage.zoom(
154 d,
155 1. / self.level,
156 mode="nearest",
157 prefilter=False)
158
159
160 def load_range(
161 lat1, lon1, lat2, lon2,
162 use_dem10=True):
163
164 lc_lat = min(lat1, lat2)
165 lc_lon = min(lon1, lon2)
166 uc_lat = max(lat1, lat2)
167 uc_lon = max(lon1, lon2)
168
169 #
170 thr = 2000 * 2000
171 #
172 dummy1, dummy2, xcells, ycells, dummy3, dummy4 = \
173 _calc_cellnums(lc_lat, lc_lon, uc_lat, uc_lon)
174 level = 1
175 cell_sizer = _DownSizer(level)
176 whole_sizer = _DownSizer(level)
177 cdivs0 = [1] + _common_divisors(_shape[0], _shape[1])
178 cdivs1 = [1] + _common_divisors(
179 _shape[0] * ycells, _shape[1] * xcells)
180 for lev in cdivs1:
181 if (_shape[0] * ycells * _shape[1] * xcells) / (lev * lev) > thr:
182 level = lev
183 for lev in cdivs0:
184 if lev <= level:
185 cell_sizer = _DownSizer(lev)
186 whole_sizer = _DownSizer(level / lev)
187 #
188 ms = 5 * cell_sizer.level * whole_sizer.level
189 _logger.info("mesh size: 5m x ({} x {}) = {}m".format(
190 cell_sizer.level,
191 whole_sizer.level,
192 ms))
193 #
194 elevs, lc, uc = _load_range0(
195 lc_lat, lc_lon, uc_lat, uc_lon,
196 convert_fun=cell_sizer, use_dem10=use_dem10)
197 #
198 elevs = whole_sizer(elevs)
199 _logger.info("shape before clip: (%d, %d)" % elevs.shape)
200
201 X = np.linspace(lc[1], uc[1], elevs.shape[1])
202 Y = np.linspace(lc[0], uc[0], elevs.shape[0])
203 xmin, xmax = np.where(X <= lc_lon)[0][-1], np.where(X >= uc_lon)[0][0]
204 ymin, ymax = np.where(Y <= lc_lat)[0][-1], np.where(Y >= uc_lat)[0][0]
205 elevs = elevs[ymin:ymax, xmin:xmax]
206 X, Y = X[xmin:xmax], Y[ymin:ymax]
207 _logger.info("shape after clip: (%d, %d)" % elevs.shape)
208 _logger.info("area size (aprx.): W-E: %dm, S-N: %dm" % (
209 elevs.shape[1] * ms,
210 elevs.shape[0] * ms))
211
212 return X, Y, elevs
まず本題でない改造から。いい加減 print をやめて logging に。convert_fun を呼び出すタイミングをもう少し早くする。具体的には、DEM5 と DEM10 をマージしてから呼び出すのではなく、各々を先に縮小する。この方がいっときに必要なメモリは少し減る。(ただしこれは同じ結果にはならない。当たり前。でも気にしない。)
本題の方。
load_range はもう convert_fun を受け取らない。_calc_cellnums は元々 _load_range0 の中にいたコード。縮小率の計算で必要なので切り出し。_common_divisors はこれ。class _DownSizer そのものは自明でしょう、みりゃわかる。
で、縮小率の決定部分は、要素数を基準に一定サイズを超えていたら縮小するように計算してる。2000×2000というのは経験則に過ぎない。10000×10000 くらいになれば、PC が固まるくらいムゴいことになるはず、普通のスペックの PC ならば。だからここらまで行ってしまうのは論外。丁度いいサイズはそういう「限界」で決まるのではなくて、「広域を見たいんだから詳細はいらんのでしょう」というバランス、な。一体どこのどいつが「500km四方を眺めたい」ときに 5m を気にすると言うのだ、ってハナシ。
「アルゴリズムらしきもの」は、「とにかく割り切れる範囲内でベストエフォート」という意味では十分に賢いとは思うけれど、「割り切れる範囲内で」というのがさ、思ったよりもずっと制約なのよ。酷いケースでは、ある領域Aの4倍の大きさの領域Bという関係の際、領域Bの方が縮小率が小さい、ということも起こりうる。つまり「セルの最大縮小率 75」をかけたあとにさらに1/2に縮小出来るか出来ないかによって。
2回目の縮小はセル結合の後の縮小なので、割り切れることにこだわらなくてもいいんだけどね。でもそうすると zoom から出る警告はうるさいし、後続の処理もあんまり気持ち良くないのでね。まぁここは考え方次第だわ。
で、「関東平野ほぼ全域」を作る例:
1 # -*- coding: utf-8 -*-
2 import numpy as np
3 import converted_loader
4 import sys
5 import logging
6 logging.basicConfig(
7 stream=sys.stdout, level=logging.INFO)
8 _logger = logging.getLogger(__name__)
9
10
11 lat_min = 34.590707
12 lat_max = 36.797053
13 lon_min = 138.488159
14 lon_max = 140.888895
15
16 #
17 _logger.info("lat_min = %.6f" % lat_min)
18 _logger.info("lat_max = %.6f" % lat_max)
19 _logger.info("lon_min = %.6f" % lon_min)
20 _logger.info("lon_max = %.6f" % lon_max)
21
22 X, Y, elevs = converted_loader.load_range(
23 lat_max, lon_max,
24 lat_min, lon_min)
25
26 elevs[np.isnan(elevs)] = np.nanmin(elevs)
27
28 #
29 import matplotlib
30 import matplotlib.cm as cm
31 import matplotlib.pyplot as plt
32 from mpl_toolkits.axes_grid1 import make_axes_locatable
33
34 elevs = np.flipud(elevs)
35
36 fig, ax = plt.subplots()
37 fig.set_size_inches(16.53 * 2, 11.69 * 2)
38
39 from matplotlib.colors import LightSource
40 ls = LightSource(azdeg=180, altdeg=15)
41 rgb = ls.shade(elevs, cm.rainbow)
42 cs = ax.imshow(elevs)
43 ax.imshow(rgb)
44
45 # create an axes on the right side of ax. The width of cax will be 2%
46 # of ax and the padding between cax and ax will be fixed at 0.05 inch.
47 divider = make_axes_locatable(ax)
48 cax = divider.append_axes("right", size="2%", pad=0.05)
49 fig.colorbar(cs, cax=cax)
50
51 ax.set_xticks([])
52 ax.set_yticks([])
53
54 #
55 plt.savefig("kanto-heiya.pdf", bbox_inches="tight")
56 #
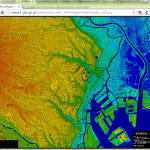
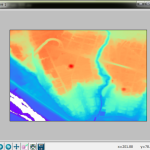
この範囲だと 1/15 (75mメッシュ)という計算になる。これで作ったのが以下:
Click here to download
1/75 でもやってみたけどさすがにこれは「汚ない」絵になる。1/25 は、ぱっと見は良くて、ちょっと拡大するとやや粗が目立つ感じ。1/15 が丁度いいと思う。まだ「抜群に解像度が高い」という印象は崩れてないから。
関東「平野」全然たいらじゃないねの巻、でした。こういうスケールで日本地図を見ると群馬は前橋、栃木は那須塩原手前まで関東平野が続くようにみえるわけだけど、こうやって細かい高度差まで描画すると、前橋も那須塩原手前も随分なだらかに高度上げてる。にしても、赤城・榛名は目立つねぇ。