もはや誰も読んでなかろうと関係ない、言い続けたいことは言い続けたい。
来週にも再度緊急事態宣言発令となりそうな今、改めて考えておくべきことはないか。
(10)というのが「重傷者数・死者数の推移予測」に関係する話だったわけだけれど、その死者数の方に関してのみのもう少し詳細。ていうか「致死率は?」
今更、ということでもあるのだが、このシリーズでワタシがずっと主張してきてるのは「伝えとらんやんけ」であって、「受け取っておらん貴様ら底辺のやつらなんか死んじまえ」ではない。わたしはどこぞの「自称毒舌落語家」ではないのだから。若者やバカモノが「理解してない」ことを責めようとはとてもじゃないけど思わんのよ。テレビが責務放棄して他人事ドリブンな批判に徹しちゃってるからね。
で、「伝えとらんやんけ」の主たるものは「実際の逼迫度」と「変化のスピード(←つまり予測に関係)」なのだが、よくよく考えたら「致死率」などのような、正しく怖れるための基礎データについてすら、ちゃんと行き届くように伝える努力を報道はしてないよなと。そして、そのことが遠因となって、「少し調べればコロナはただの風邪だとわかります」のような「正しいデマ」がまかり通る隙を与えてしまうのだ。
「正しいデマ」という言い方をするのは、無論「正しい」からである。風邪と同じコロナウィルスだ。その通り。どこがデマかと言えば、(その主張をしたい者にとっての)「不都合な真実」について何も語っていないこと、だ。「言っている部分だけに限れば正しい」ということに過ぎない。
そんなことをずっと思っていたのだが、一般人が簡単に手に出来るデータ(=東洋経済オンラインWEBのデータ)だけで知ろうとする場合、致死率や重症化率、年代別比などは、厄介もしくは「不可能」だったりもして、なんというか「出来ることしか出来ない」んだよね。それでも、都道府県別の致死率実績自体はほぼ正確に求めることが出来て、本日時点までの実績を用いると、およそこんな値になる:
1 北海道 3.6 %
2 青森県 1.5 %
3 岩手県 3.9 %
4 宮城県 0.7 %
5 秋田県 2.3 %
6 山形県 2.2 %
7 福島県 3.6 %
8 茨城県 1.7 %
9 栃木県 1.4 %
10 群馬県 1.8 %
11 埼玉県 2.0 %
12 千葉県 1.9 %
13 東京都 1.4 %
14 神奈川県 1.6 %
15 新潟県 0.9 %
16 富山県 2.4 %
17 石川県 3.0 %
18 福井県 4.0 %
19 山梨県 1.7 %
20 長野県 1.5 %
21 岐阜県 2.4 %
22 静岡県 1.9 %
23 愛知県 2.0 %
24 三重県 2.2 %
25 滋賀県 1.8 %
26 京都府 1.6 %
27 大阪府 1.8 %
28 兵庫県 2.4 %
29 奈良県 1.2 %
30 和歌山県 1.0 %
31 鳥取県 0.6 %
32 島根県 0.0 %
33 岡山県 1.0 %
34 広島県 1.9 %
35 山口県 2.7 %
36 徳島県 2.8 %
37 香川県 1.8 %
38 愛媛県 1.4 %
39 高知県 2.0 %
40 福岡県 1.7 %
41 佐賀県 0.9 %
42 長崎県 2.2 %
43 熊本県 2.1 %
44 大分県 1.6 %
45 宮崎県 1.1 %
46 鹿児島県 1.4 %
47 沖縄県 1.1 %
48 全国 1.8 %
むろんこれは「死者数報告の累積/新規陽性者数の累積」で簡単に求まる。この値で注意すべきはもちろん、無症候キャリアが相当数想定されるため、実際の致死率はみえているこの値よりもずっと低いだろうということ、であり、おそらく「少し調べれば」論者が喜んでツッコむのもこの点だろう。
そうじゃねーだろ、と思わん? この値をみて、何をどう考えるか、の第一歩は、そう、「自覚症状があって検査に引っかかった人(感染判明者)の2% が死ぬ」ということ、ではないの? そしてこれは「人それぞれの考え方による」ものではない、まごうことなき客観的な「事実」である。スクリーニング検査が充実していない日本の場合、「感染判明者」の多数が要するに「救急搬送を要する」事態に陥っていて、「2%」の多くを占めるのがそういう人々で、であれば彼らは「2%という高い数字に平均を引き上げている人々」で、であればその彼らは「2%を遥かに超える確率で死ぬ」ということも表していて、言い換えれば「救急車に乗るような事態に陥った場合は高確率で死ぬ」ということでもある。
「正しく怖れよ」というのは、まずはこの2%の中身についてだ。この2%のほとんどが高齢者である、ということについては、「年代別の国内発生動向」をじっくり観察してみるべきだ。そして、特に「40代」に着目するべきである。「ほとんど」という言葉に注意しなければならない。「全部が」とは言ってない。
私が非常に懸念し想像しているのが、「若者は重症化しない」ということを自分事と把握している40代が相当多いであろう、ということだ。グラフをじっくり観察して欲しいが、40代は、よくても「中リスク者」であって、決して低リスク分類ではない。テレビで活躍するタレントの40代は、「中堅」と呼ばれることはあっても「大御所」や「重鎮」ではなく、これは高度成長期前の時代とは世代の感覚がまったく違っていて、「若者」と言った場合に一般市民が想像する年代は、どんどん高くなっている。この「若者」感と、COVID-19 における中リスク層40代という真実とのギャップである、これが大問題だ。(「正しく」と言っているのであって、ちゃんと実数から理解して欲しい。4月21日までに、40代が72人亡くなっていて、これは40代陽性者のおよそ0.1%、すなわち1000人に一人である。)
「テレビを観ない」というか、「ええことを言ってるワイドショー」を視聴できない「日本を支えている働き盛り」が、「ワタシタチガコンナニイイコトヲイッテルノニ!!」と責められてはいかんわけよ、ちゃんと「あなたたち40代もちゃんと危険年代なんだぞ」てことを、なんなら毎日伝えなきゃいかんのじゃないの? と、ワタシは思うわけだ。
「正しく怖れよ」の「正しく」の二つ目は無論「軽症・中等症とはどんな状態なのか」に関してと「後遺症」についてだ。これも「日本を支えている働き盛り」がテレビを見ない時間に「危険なんだぞー大変なんだぞー」と。ええ加減にせえよ、と思う。肺炎の自覚症状があって息苦しくて、本人は死を覚悟するほどにキツいのに「軽症」なのだ、という実状。「ちょっと調べれば風邪」論者はこの真実について決して触れない。「重症化率が低い」という正しい事実があれば「ちょっと調べれば風邪」として成立するのだから、それでいいわけだ。
「ちょっと調べれば風邪」論者は、無垢にそれを信じているのか、それとも悪意があるのかはわからん。それよりも、その「ちょっと調べれば風邪」論者を信じてしまう受け手が、どうしてそういう事態に陥るか、という点についても、ちゃんと考えた方がいい。これは心理学の領域である。「人間は誰しも、(意識して自覚しない限りは)自分の意見に沿う都合のいい情報だけを無意識に集めてしまう」。こういう人をただ責めるだけではなく、そういう相手にも届くように伝えなければならない、ということ。これは非常に厄介な問題である。
「正しく怖れよ」の「正しく」の3つ目。まぁこれを言いたくて今回のネタを書こうと思ったのよね。「2%」とはどんな値なのか、だよ。その内容じゃなくて。
既に上で書いたのだ。「感染判明者の2%」だと。集合論の素養が…なんて話をしたいところだが、それよりも、学校を想像してみるとわかりやすい。
まず、感染リスクのない、つまり一人も感染者がいない学校にあなたがいるとする。この場合に、外部からのリスクが持ち込まれないとしたら、この学校内で新型コロナ感染で死亡する確率は? そう。0%である。「2% 死ぬんじゃないのか?」。いや、だから言ったじゃないか。「感染判明者の2%」なのだと。
次に、感染者が既に全校生徒600人のうち300人いる学校にいて、あなたが未感染者だとする。この場合、あなたが感染しないとしたら、この学校内で新型コロナ感染で死亡する確率は? そう。0%である。「2% 死ぬんじゃないのか?」。いや、だから言ったじゃないか。「感染判明者の2%」なのだと。
感染症とその確率を考える場合、今の場合「2%死ぬ」をどうイメージすればいいかといえばこれは、「命中すれば致死率 100% のライフルを持つ、2%命中率のハンター」みたいなことだ。ハンターに遭遇しなければ死ぬことはないし、遭遇しても見つからなければ死なない確率が高まる。けれども「見つかって、狙われて撃たれれば2%死ぬ」のだ。だから、学校の例でいえば、後者の例の方がはるかに「2% と仲良し」であり、非常にリスクが高い。周りがハンターだらけになっている、ということだからだ。また、自身が感染者になることがその「2%ハンターになる」ということでもある。
「自覚症状があって検査に引っかかった人の 2% が死ぬ」という前段の「自覚症状があって」に至る確率が高まれば高まるほど「2%死ぬまっしぐら」だが、仮にその前段を満たした、つまり「感染した」としたら? 改めて2%の意味を思い知るがいい。同じく学校で。30人学級で、一学年3クラス、六学年、として、およそ540人、この2%とは、11人である。小学校全体で11人のうちの一人にならない自信はあるか? 一学年に二人のうちの一人にならない自信はあるか? (ちなみにワタシは全校生徒1000人くらいの中で10人以内に入った経験が最低でも二つある。) というか、そもそも小学校で11人が一気に亡くなったらこれはもう大惨事であろうよ。
「オリンピック選手級」と「お山の大将」の、どちらになるのが簡単か、を想像すると、もっと身近に感じるかもしれない。一学年に二人、という数字はまさに「お山の大将」に近い比率、だと思わんか? 「ガキ大将」ならどこにでもいても、そのガキ大将全てが K-1 王者級になるのではない。「2%死ぬ」という確率は、K-1 王者になるほどに稀な確率などではなく、たかだかガキ大将レベルなのだ。
感染症の感染制御とは要するに、「2% がやってこないようにする」ことである。集団の行動によって大きく影響されるために、どうしても「あんたがどう思おうと」皆で協力して行動を決定する必要がある、ということだ。ワクチンによって集団免疫を獲得するまでは。そう、「感染しなけりゃいい」し、「そのためには周りが感染してなきゃいい」のだ。これこそが「ステイホーム」の根拠なのだ、てことだ。
正しく怖れるのであるから、たとえば自分が基礎疾患のない10代である場合にさえも自身の死の恐怖に怯える必要があるかといえば、それはない。実際現在までの20代未満の死者が日本でほとんど出ていない。けれども、感染したあなたは「2% ハンター」であり、身近な高齢者を撃ち殺してしまうことは怖れなければならない。学生が、中高年の両親を殺してしまうとして、先立つものはあるか? 学校には通い続けられるか? これについての想像を巡らせて怯えよ、ということである。
正しく怖れよとはつまり、「かかってはいけない」という大原則と、その感染防御を知る、ということであって、決して「かかっても所詮風邪、世間は怖れすぎであると知ること」ではない。航空機事故で死ぬ確率と比較することが正しい怖れ方である、という主張を鵜吞みにしないことである。そもそも航空機事故と違って、「我々自身で制御出来る」のだ。制御を知ることこそが「正しい怖れ方」なのである。
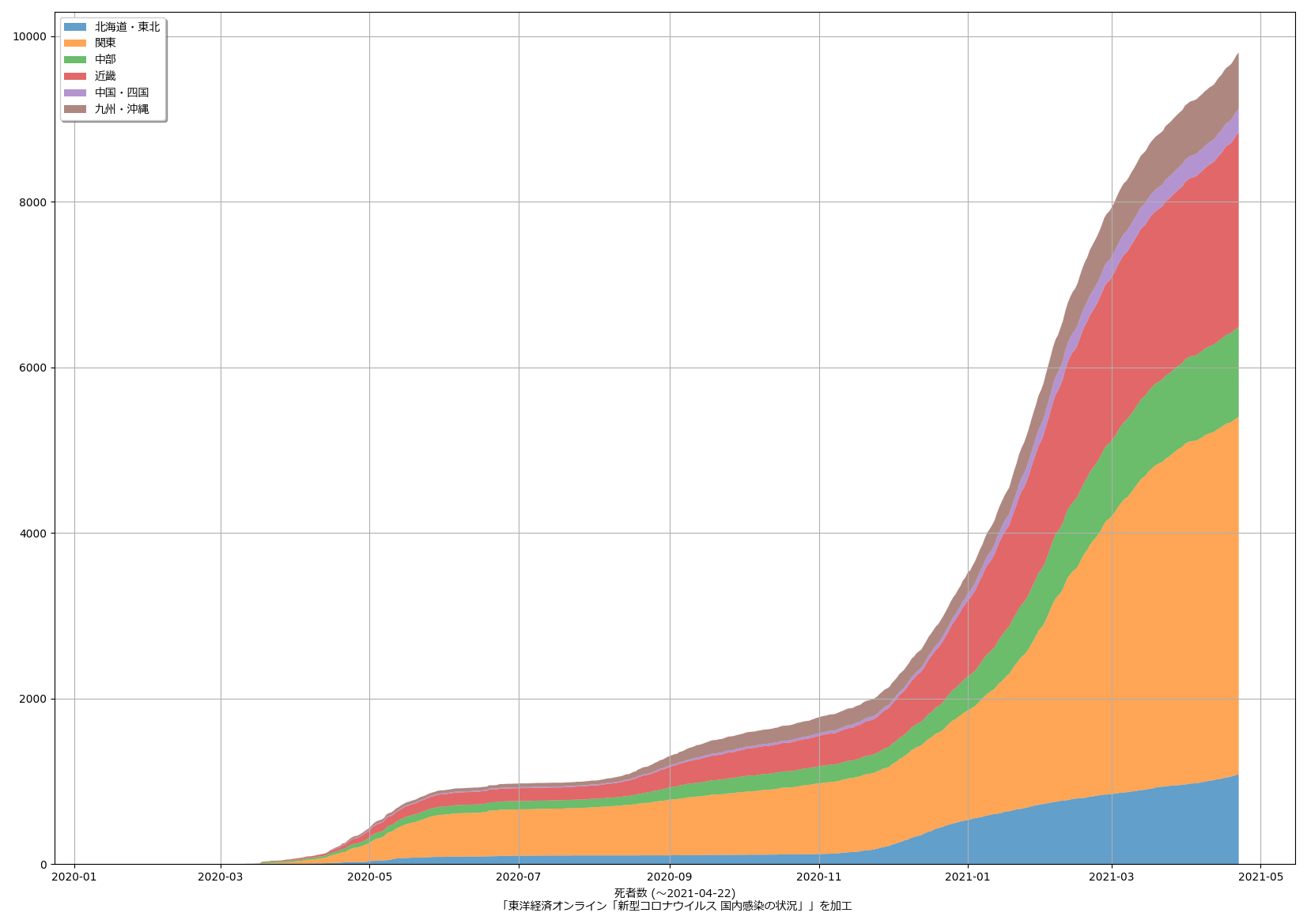
「致死率」よりも「死者数」で示された方がイメージしやすい人もいるかもしれないので一応:
1 # -*- coding: utf-8 -*-
2 import io
3 import datetime
4 import functools
5 import numpy as np
6 import csv
7 import matplotlib as mpl
8 import matplotlib.pyplot as plt
9 import matplotlib.font_manager
10
11
12 _PREFCODE = {
13 '北海道': 1,
14 '青森県': 2,
15 '岩手県': 3,
16 '宮城県': 4,
17 '秋田県': 5,
18 '山形県': 6,
19 '福島県': 7,
20 '茨城県': 8,
21 '栃木県': 9,
22 '群馬県': 10,
23 '埼玉県': 11,
24 '千葉県': 12,
25 '東京都': 13,
26 '神奈川県': 14,
27 '新潟県': 15,
28 '富山県': 16,
29 '石川県': 17,
30 '福井県': 18,
31 '山梨県': 19,
32 '長野県': 20,
33 '岐阜県': 21,
34 '静岡県': 22,
35 '愛知県': 23,
36 '三重県': 24,
37 '滋賀県': 25,
38 '京都府': 26,
39 '大阪府': 27,
40 '兵庫県': 28,
41 '奈良県': 29,
42 '和歌山県': 30,
43 '鳥取県': 31,
44 '島根県': 32,
45 '岡山県': 33,
46 '広島県': 34,
47 '山口県': 35,
48 '徳島県': 36,
49 '香川県': 37,
50 '愛媛県': 38,
51 '高知県': 39,
52 '福岡県': 40,
53 '佐賀県': 41,
54 '長崎県': 42,
55 '熊本県': 43,
56 '大分県': 44,
57 '宮崎県': 45,
58 '鹿児島県': 46,
59 '沖縄県': 47,
60 }
61 _REGIONS = [
62 ("北海道・東北",
63 ("北海道", "青森県", "岩手県", "宮城県",
64 "秋田県", "山形県", "福島県",)),
65 ("関東",
66 ("茨城県", "栃木県", "群馬県",
67 "埼玉県", "千葉県", "東京都", "神奈川県",)),
68 ("中部",
69 ("山梨県", "長野県", "新潟県", "富山県",
70 "石川県", "福井県", "静岡県", "愛知県", "岐阜県",)),
71 ("近畿",
72 ("三重県", "滋賀県", "京都府", "大阪府",
73 "兵庫県", "奈良県", "和歌山県",)),
74 ("中国・四国",
75 ("鳥取県", "島根県", "岡山県", "広島県",
76 "山口県", "香川県", "愛媛県", "徳島県", "高知県",)),
77 ("九州・沖縄",
78 ("福岡県", "佐賀県", "長崎県", "熊本県",
79 "大分県", "宮崎県", "鹿児島県", "沖縄県",)),
80 ]
81 def _vis(dattko):
82 fontprop = matplotlib.font_manager.FontProperties(
83 fname="c:/Windows/Fonts/meiryo.ttc")
84
85 era = "2020/1/16" # 木曜日
86 era = datetime.date(*map(int, era.split("/")))
87 #
88 k = "deaths_cumulative"
89 d = dattko[k]
90 T = [era + datetime.timedelta(t) for t in range(len(d))]
91 #
92 fig, ax1 = plt.subplots(tight_layout=True)
93 fig.set_size_inches(16.53, 11.69)
94 sums = [
95 np.nansum([d[:,_PREFCODE[pn] - 1] for pn in ps], axis=0)
96 for r, ps in _REGIONS]
97 ax1.stackplot(T,
98 sums, labels=[r for r, ps in _REGIONS],
99 alpha=0.7)
100 ax1.legend(loc="upper left", shadow=True, prop=fontprop)
101 ax1.set_xlabel(
102 "死者数 (~{})\n「東洋経済オンライン「新型コロナウイルス 国内感染の状況」」を加工".format(
103 str(T[-1])),
104 fontproperties=fontprop)
105 ax1.grid(True)
106 fig.savefig("{}_{}_stackplot.png".format(
107 k, str(T[-1]).replace("-", "")[4:]))
108 plt.close(fig)
109
110
111 if __name__ == '__main__':
112 _vis(np.load(io.open("toyokeizai_online_covid19.npz", "rb")))
とまぁ「致死率2%」という値が弾き出されて、ワタシ自身も少しばかり驚いたので、ちょっとうるさく言ってみた。
ネタとしての(10)からの続き、としては、「新規感染判明から死に至るまでのタイムラグ」について、改めてやってみようと思ったのだ。少し違った方法を使って。随分試行錯誤を経たが、結果としてはこんなコード:
1 # -*- coding: utf-8 -*-
2 # toyokeizai_online_covid19.npz などについてはあとで貼り付ける zip 内参照。
3 import io
4 import datetime
5 import numpy as np
6 import matplotlib.pyplot as plt
7 import matplotlib.font_manager
8
9
10 def _get_delay(adv, dst):
11 # 2つのデータの関係を大雑把に把握。山の形の差異のみで推定する、ということ
12 # だが、山の尖り方の違いがあるので、ほんとうに大雑把にしかわからない。
13 an = adv / adv.max()
14 dn = dst / dst.max()
15 diffmin = np.inf
16 delay = 5
17 for d in range(delay, 30):
18 diff = np.nansum(abs(np.roll(an, d) - dn)[d:])
19 if diff < diffmin:
20 delay = d
21 diffmin = diff
22 #print("{:3d}".format(delay), "{:7.2f}".format(diffmin))
23 return delay
24
25
26 def _vis(dattko):
27 #
28 era = datetime.date(2020, 1, 16)
29 skip = 0 #7*4*8
30 #
31 fontprop = matplotlib.font_manager.FontProperties(
32 fname="c:/Windows/Fonts/meiryo.ttc")
33
34 era = "2020/1/16" # 木曜日
35 era = datetime.date(*map(int, era.split("/")))
36 # 新規感染判明から死亡に至るまでに要する日数の推定 (120日間データで推定)
37 ddtargdays = 120
38 ddelay = _get_delay( # 本日2021-04-21時点で「23日」と求まる。
39 np.nansum(dattko["testedPositive_movavg"], axis=1)[-ddtargdays:],
40 np.nansum(dattko["deaths_movavg"], axis=1)[-ddtargdays:])
41 #
42 for (wh_sl, wh_n) in (
43 (slice(12, 12+1), "東京"),
44 (slice(3, 3+1), "宮城"),
45 (slice(26, 26+1), "大阪"),
46 (slice(29, 29+1), "和歌山"),
47 (slice(0, 47), "全国")):
48 fig, ax1 = plt.subplots(tight_layout=True)
49 fig.set_size_inches(16.53 * 2, 11.69)
50 ax2 = ax1.twinx()
51 T = np.array([era + datetime.timedelta(t)
52 for t in range(len(dattko["deaths"]))])
53 ax1.set_xlim((T[skip], T[-1]))
54 ax1.set_ylabel("死亡者数", fontproperties=fontprop)
55 ax2.set_ylabel(
56 "新規感染者報告数".format(ddelay), fontproperties=fontprop)
57 #
58 Y1 = np.nansum(dattko["deaths_movavg"][:,wh_sl], axis=1)
59 Y2 = np.nansum(dattko["testedPositive_movavg"][:,wh_sl], axis=1)
60 Y3 = np.roll(Y2, ddelay)[ddelay:]
61 l1, = ax1.plot(T, Y1, color="tab:red", linestyle="dashed")
62 l2, = ax2.plot(T, Y2, color="tab:blue", alpha=0.025)
63 ax2.fill_between(T, Y2, color="tab:blue", alpha=0.025)
64 l3, = ax2.plot(T[ddelay:], Y3, color="tab:blue", linestyle="dotted")
65 ax1.legend(
66 (l1, l2, l3),
67 ("死亡者数", "新規感染者報告数", "{}日前の新規感染者報告数".format(ddelay)),
68 shadow=True, prop=fontprop)
69 ax1.grid(True)
70 ax1.set_title(
71 "{}\n「東洋経済オンライン「新型コロナウイルス 国内感染の状況」」を加工".format(
72 wh_n),
73 fontproperties=fontprop)
74 fig.savefig("dd_{}_{}.png".format(str(T[-1]), wh_n))
75 #plt.show()
76 plt.close(fig)
77 # -----
78
79
80 if __name__ == '__main__':
81 _vis(np.load(io.open("toyokeizai_online_covid19.npz", "rb")))
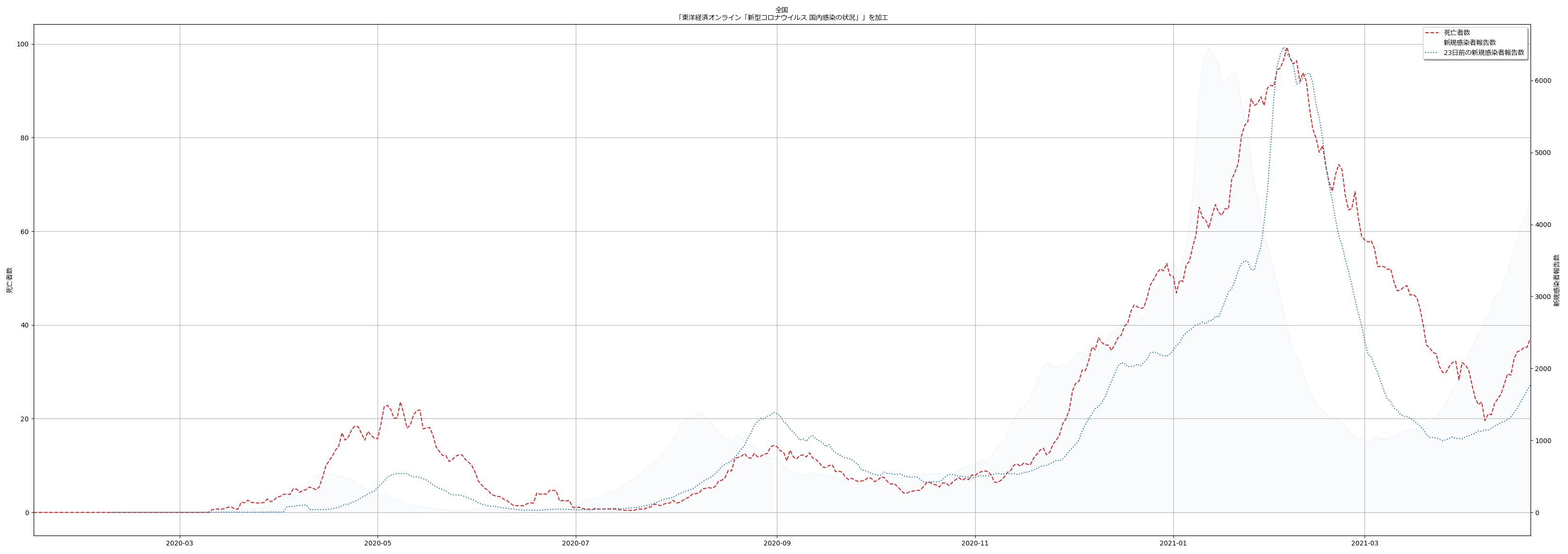
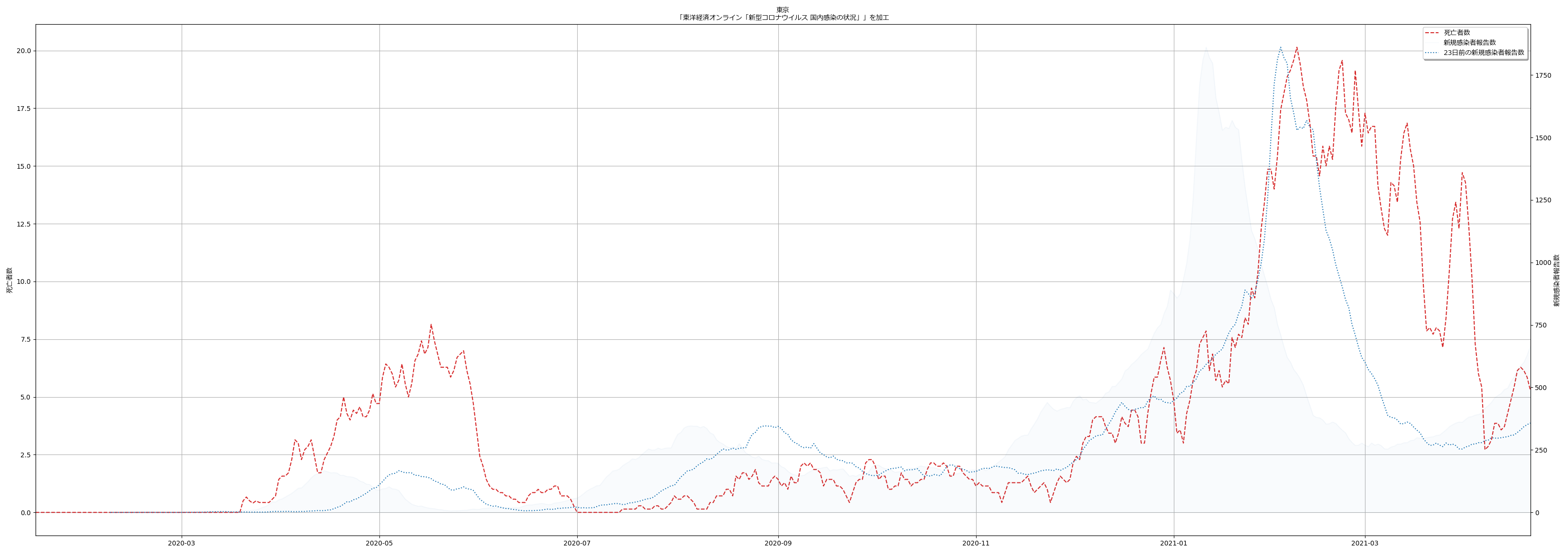
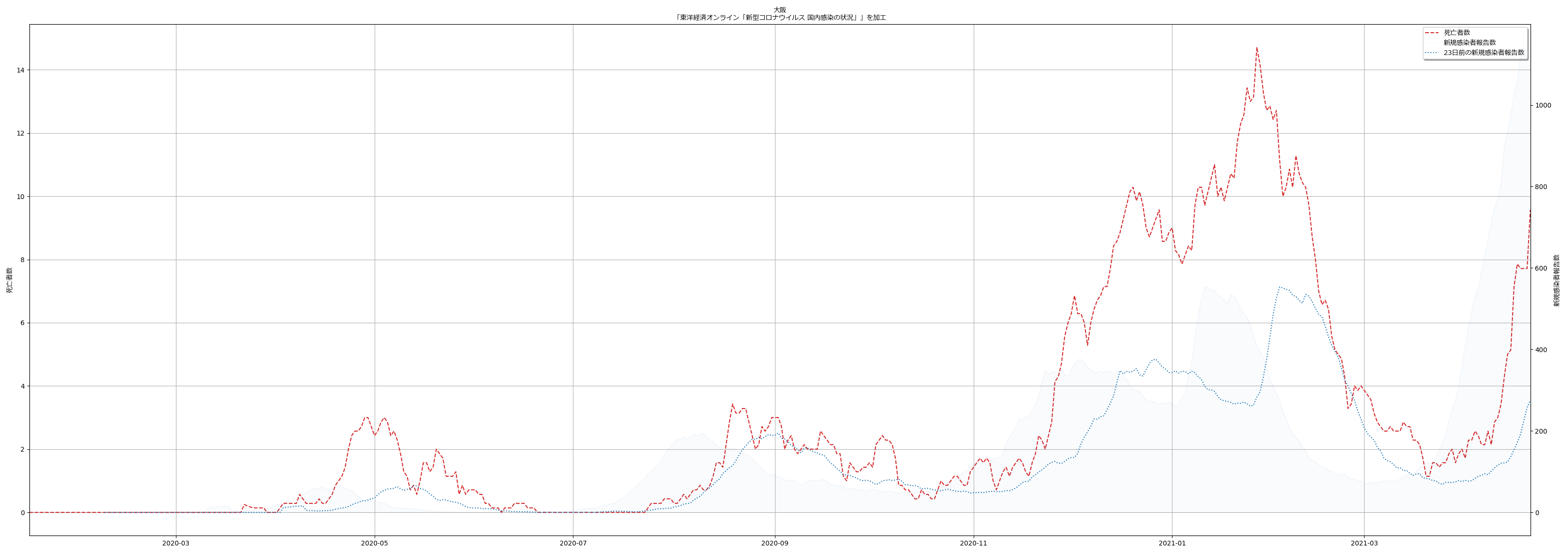
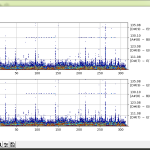
陽性判明から 23 日で亡くなってしまうというのは、感覚的にはかなり早い気がする。かなり雑な判定方法で探り当てているが、専門家の人たちが言っていたことと概ね一致してるので、おそらくおおよそ正しいのだろう。というわけで、「死亡者数報告は、新規陽性者報告から23日遅れて出てくる」ということを理解しておけば、医療の逼迫度合いがどのように推移するのかの、ある程度の予測に役立つかもしれない。(ほんとはこれは重傷者でこそ知るべきなんだけど、オープンなデータだけだとこれは困難。)
ここまでは「役に立つかもしれない」話だったが、次に、「役に立つかどうかわからない」話を。
上の _get_delay で「感染判明から23日で死亡する」という「中心」がわかったのだから、これを使って「死亡率の推移」というものがわからないだろうか、と思ったのだ。つまり、「死亡者数/23日前の新規感染者数報告」を可視化することは、何かを言うことにつながるであろうか、と:
1 # -*- coding: utf-8 -*-
2 import io
3 import datetime
4 import csv
5 import numpy as np
6 import matplotlib.pyplot as plt
7 import matplotlib.font_manager
8 import matplotlib.ticker as ticker
9 from matplotlib.colors import BoundaryNorm, Normalize
10
11
12 class MidpointNormalize(Normalize):
13 def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
14 self.vcenter = vcenter
15 Normalize.__init__(self, vmin, vmax, clip)
16
17 def __call__(self, value, clip=None):
18 # I'm ignoring masked values and all kinds of edge cases to make a
19 # simple example...
20 x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
21 return np.ma.masked_array(np.interp(value, x, y))
22
23
24 _PREFCODE = {
25 '北海道': 1,
26 '青森県': 2,
27 '岩手県': 3,
28 '宮城県': 4,
29 '秋田県': 5,
30 '山形県': 6,
31 '福島県': 7,
32 '茨城県': 8,
33 '栃木県': 9,
34 '群馬県': 10,
35 '埼玉県': 11,
36 '千葉県': 12,
37 '東京都': 13,
38 '神奈川県': 14,
39 '新潟県': 15,
40 '富山県': 16,
41 '石川県': 17,
42 '福井県': 18,
43 '山梨県': 19,
44 '長野県': 20,
45 '岐阜県': 21,
46 '静岡県': 22,
47 '愛知県': 23,
48 '三重県': 24,
49 '滋賀県': 25,
50 '京都府': 26,
51 '大阪府': 27,
52 '兵庫県': 28,
53 '奈良県': 29,
54 '和歌山県': 30,
55 '鳥取県': 31,
56 '島根県': 32,
57 '岡山県': 33,
58 '広島県': 34,
59 '山口県': 35,
60 '徳島県': 36,
61 '香川県': 37,
62 '愛媛県': 38,
63 '高知県': 39,
64 '福岡県': 40,
65 '佐賀県': 41,
66 '長崎県': 42,
67 '熊本県': 43,
68 '大分県': 44,
69 '宮崎県': 45,
70 '鹿児島県': 46,
71 '沖縄県': 47,
72 }
73 _PREFCODE_r = {pc: pcn for pcn, pc in _PREFCODE.items()}
74
75
76 def _get_facs_as_tokyo():
77 reader = csv.reader(io.open("pp.txt", encoding="cp932"), delimiter="\t")
78 fac = []
79 for row in reader:
80 fac.append((_PREFCODE[row[1]], int(row[4].replace(",", ""))))
81 fac.sort()
82 return np.array([(n / fac[12][1]) for pc, n in fac])
83
84
85 def _get_delay(adv, dst):
86 # 2つのデータの関係を大雑把に把握。山の形の差異のみで推定する、ということ
87 # だが、山の尖り方の違いがあるので、ほんとうに大雑把にしかわからない。
88 an = adv / adv.max()
89 dn = dst / dst.max()
90 diffmin = np.inf
91 delay = 5
92 for d in range(delay, 30):
93 diff = abs(np.roll(an, d) - dn)[d:].sum()
94 if diff < diffmin:
95 delay = d
96 diffmin = diff
97 #print("{:3d}".format(delay), "{:7.2f}".format(diffmin))
98 return delay
99
100
101 def _vis(dattko):
102 #
103 era = datetime.date(2020, 1, 16)
104 skip = 7*4*6 + 14
105 #
106 fac = _get_facs_as_tokyo()
107 #
108 fontprop = matplotlib.font_manager.FontProperties(
109 fname="c:/Windows/Fonts/meiryo.ttc")
110
111 # 新規感染判明から死亡に至るまでに要する日数の推定 (120日間データで推定)
112 ddtargdays = 120
113 ddelay = _get_delay( # 本日2021-04-21時点で「23日」と求まる。
114 np.nansum(dattko["testedPositive_movavg"], axis=1)[-ddtargdays:],
115 np.nansum(dattko["deaths_movavg"], axis=1)[-ddtargdays:])
116 #
117 era = "2020/1/16" # 木曜日
118 era = datetime.date(*map(int, era.split("/")))
119 totdays = len(dattko["testedPositive"])
120 T = np.array([era + datetime.timedelta(t) for t in range(totdays)])
121 for pc in range(48):
122 if pc < 47:
123 wh_n = _PREFCODE_r[pc + 1]
124 wh_sl = slice(pc, pc + 1)
125 else:
126 wh_n = "全国"
127 wh_sl = slice(0, 47)
128 k = "testedPositive_movavg"
129 # -----
130 # 新規陽性者, 前週比
131 Z0 = np.nansum(dattko[k][:,wh_sl], axis=1)
132 Z0r = np.nansum(dattko["testedPositive"][:,wh_sl], axis=1)
133 Z1 = np.array(Z0)
134 Z1[np.where(
135 np.logical_and(Z1 < 1, np.roll(Z1, 7, axis=0) < 1))] = np.nan
136 Z1[np.where(Z1 < 1)] = 1
137 Z1 /= np.roll(Z1, 7, axis=0)
138 Z1[np.where(np.isnan(Z1))] = 0
139 # -----
140 # 死亡者数/ddelay日前の新規感染者数報告。何かの目安になるであろうか??
141 de = np.nansum(dattko["deaths_movavg"][:,wh_sl], axis=1)
142 Z2 = (de / np.roll(Z0, ddelay) * 100)[ddelay:]
143
144 # ---------------------------------------------------
145 # ppp3.py の案2 + α
146 fig, (ax1, ax2) = plt.subplots(
147 2, 1, gridspec_kw={'height_ratios': [20, 1]}, tight_layout=True)
148 fig.set_size_inches(16.53 * 1.2, 11.69)
149 # 「死亡者数/ddelay日前の新規感染者数報告」と違って、全期間での総和同士
150 # に基づく死亡率計算はこれは「真実」(実績)を(ほぼ)直接表現する。
151 dr = 100 * np.nansum(dattko["deaths"][:,wh_sl]) / np.nansum(
152 dattko["testedPositive"][:,wh_sl])
153 print(wh_n, "{:.1f} %".format(dr))
154 ax1.set_title(
155 "{}: {}まででの致死率実績 {:.1f} %".format(
156 wh_n, str(T[-1]), dr),
157 fontproperties=fontprop)
158 ax1.plot(T, Z0)
159 ax1.bar(T, Z0r, color="tab:blue", alpha=0.1)
160 ax1.set_xlim((T[skip], T[-1]))
161 if pc == 12 or pc == 47:
162 ax1.set_ylabel("新規陽性者数", fontproperties=fontprop)
163 else:
164 ax1.set_ylabel("新規陽性者数 (括弧内は東京換算)",
165 fontproperties=fontprop)
166 ax1.yaxis.set_major_formatter(
167 lambda x, pos: "{}\n({:.1f})".format(x, x / fac[pc]))
168 ax3 = ax1.twinx()
169 ax3.plot(T[ddelay:], Z2, color="tab:red", linestyle="dashed")
170 ax3.set_ylabel(
171 "死亡者数移動平均/{}日前の新規感染者数移動平均 [%]".format(ddelay),
172 fontproperties=fontprop)
173 limmaxtarg = Z2[skip - ddelay:]
174 limmax = np.nanmax(limmaxtarg)
175 if np.isinf(limmax):
176 limmax = np.nanmax(
177 limmaxtarg[np.where(np.logical_not(np.isinf(limmaxtarg)))])
178 if not limmax or np.isnan(limmax):
179 ax3.set_ylim((0, 1))
180 else:
181 ax3.set_ylim((0, min(20, limmax)))
182 #
183 Y = np.arange(2)
184 X, Y = np.meshgrid(T, Y)
185 norm = MidpointNormalize(vcenter=0.9, vmax=2.0)
186 ax2.pcolormesh(
187 X, Y, [Z1, Z1], norm=norm, cmap="coolwarm",
188 shading="nearest") # shading: auto, nearest, gouraud
189 ax2.set_xlim((T[skip], T[-1]))
190 ax1.tick_params(
191 axis="x", bottom=False, top=True, labelbottom=False, labeltop=True)
192 #ax1.tick_params(
193 # axis="y", right=True, labelright=True)
194 ax2.set_yticks([])
195 ax2.set_xlabel(
196 "{} ({})\n「東洋経済オンライン「新型コロナウイルス 国内感染の状況」」を加工".format(
197 "新規陽性者数(折れ線は7日移動平均)", wh_n),
198 fontproperties=fontprop)
199 ax1.grid(True)
200 fig.savefig("{}_{:02d}{}_withcpw_{}_5.png".format(k, pc + 1, wh_n, str(T[-1])))
201 #plt.show()
202 plt.close(fig)
203 # -----
204
205
206 if __name__ == '__main__':
207 _vis(np.load(io.open("toyokeizai_online_covid19.npz", "rb")))
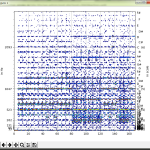
うーん、よくわからんなぁこれは:
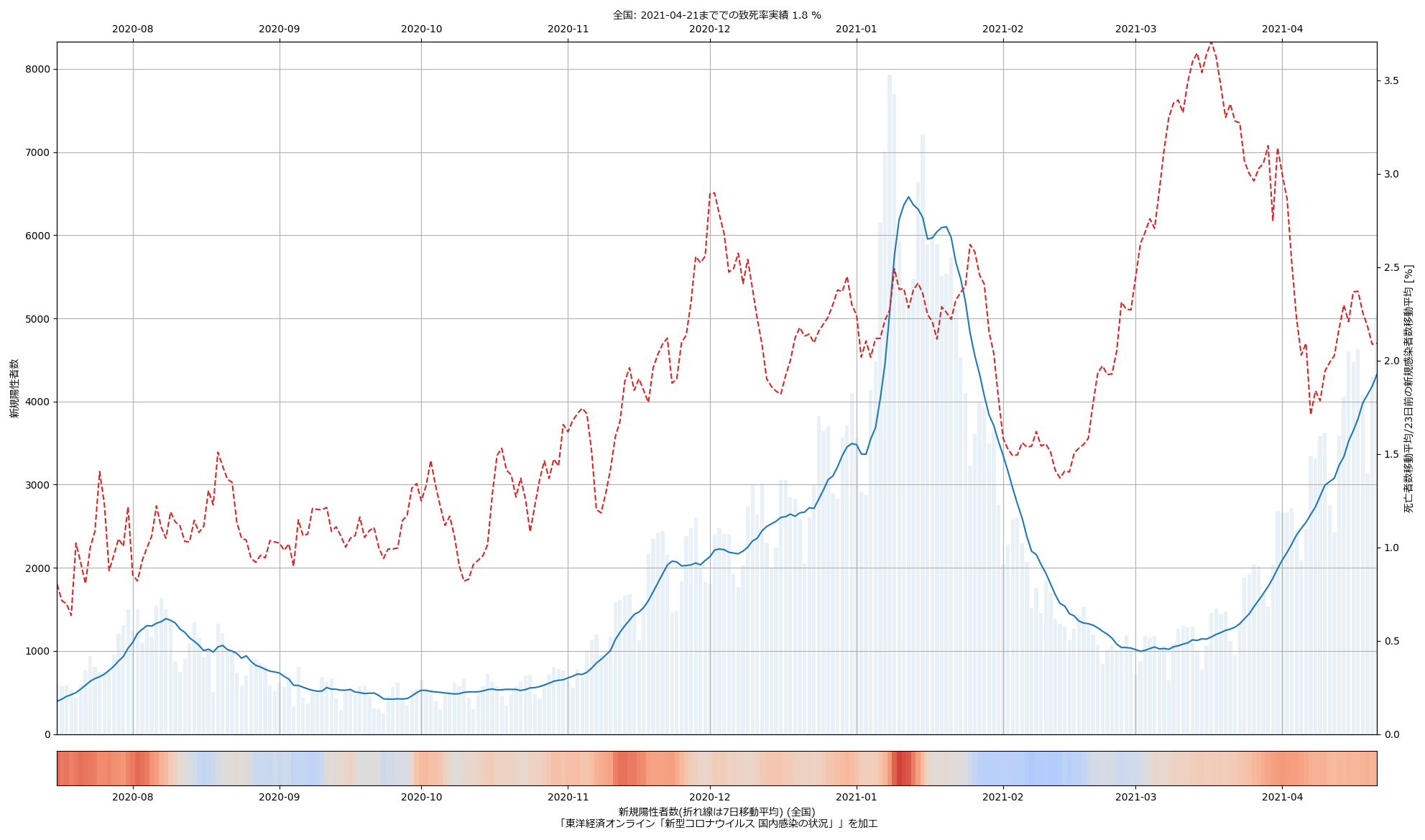
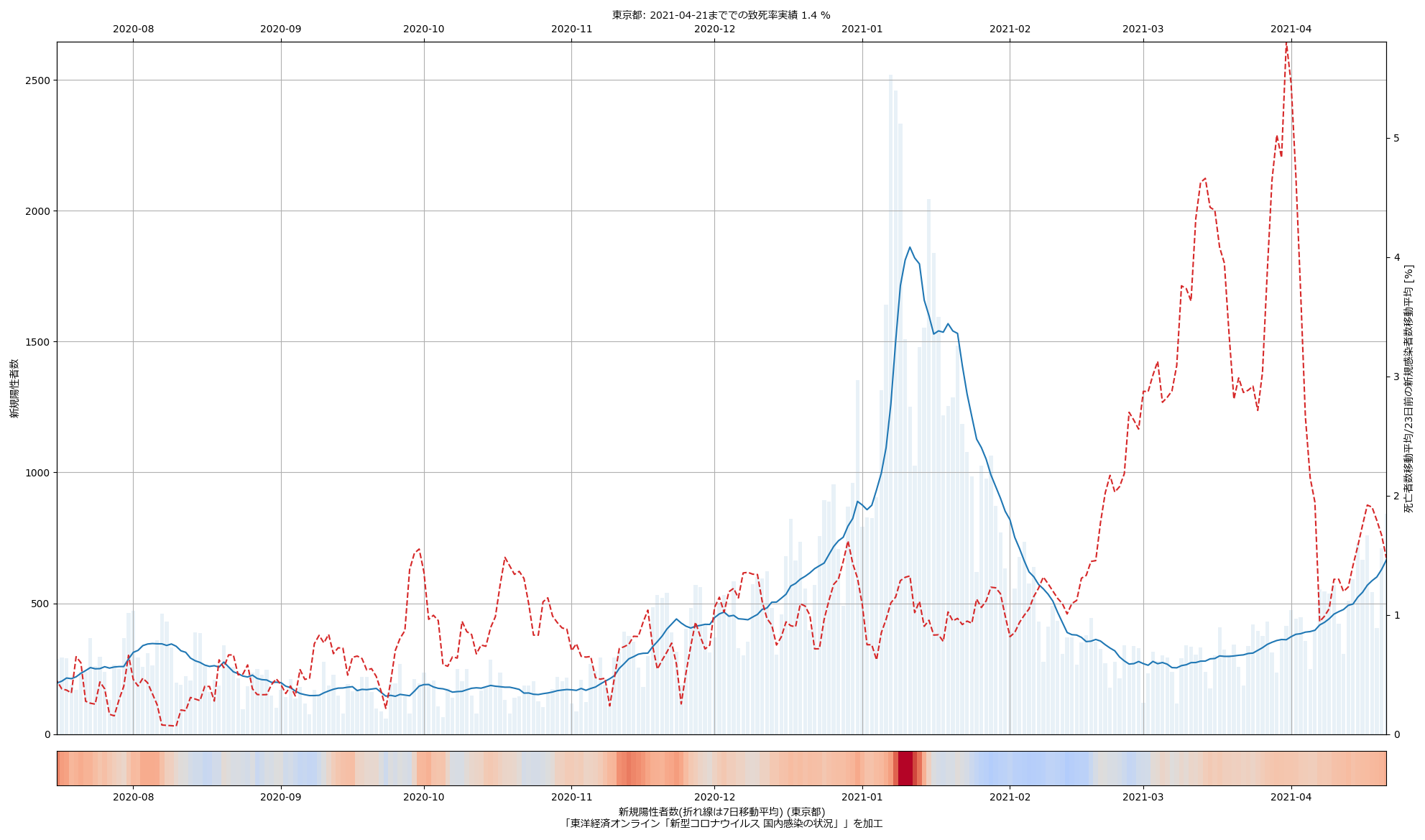
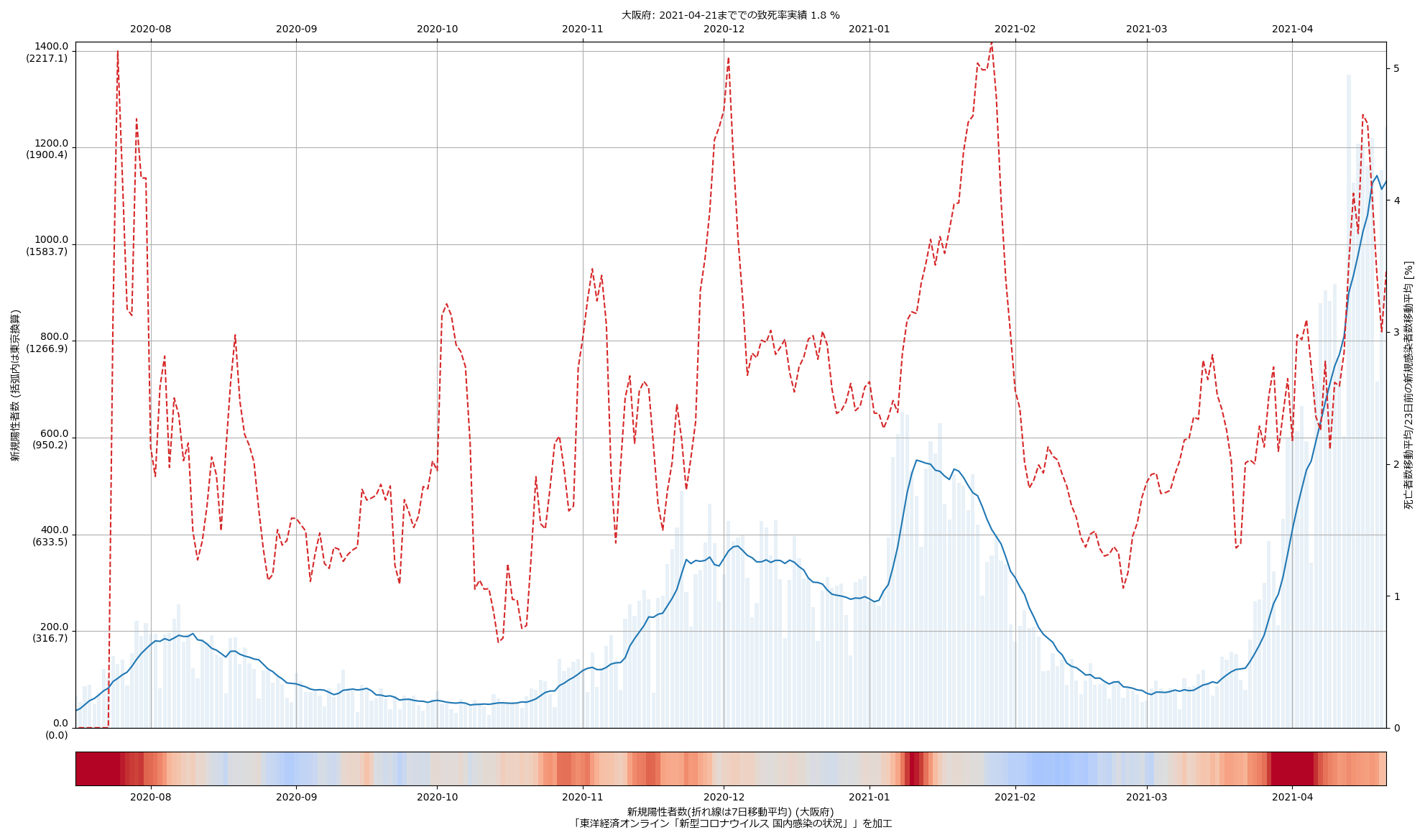
一定の値を推移してる範囲があることからみて、大間違いの値をはじき出してるということはないとは思う。問題と思うのは、この推移の意味の解読が簡単じゃない、ということ。東京の最近の値が高いことの理由は、本当に死亡率が高かったからだけとは限らない。「23日前」の感染者数が少なく、また、「23日後」という中心を大きく外れて延命していて死亡した人が多かった、など、色々考えられる。が、その「色々」の考察が、何かの注意喚起に使えたりするだろうか、と考えるも、どうにも想像つかない。つまり「役に立つ指標にはならなそうだなぁ」と。うーん…。
まぁそういうわけで、あんまりやった価値はなさそうなんだけれど、ともあれ、使ったコード全部: viz_cpv19data_scratch_20210422.zip
今回の以外のヤツも全部入ってる。例によって滅茶苦茶な名前(pppp5.py とか)なのでご覚悟を。一応最新データでの cov19viz446.py 結果:

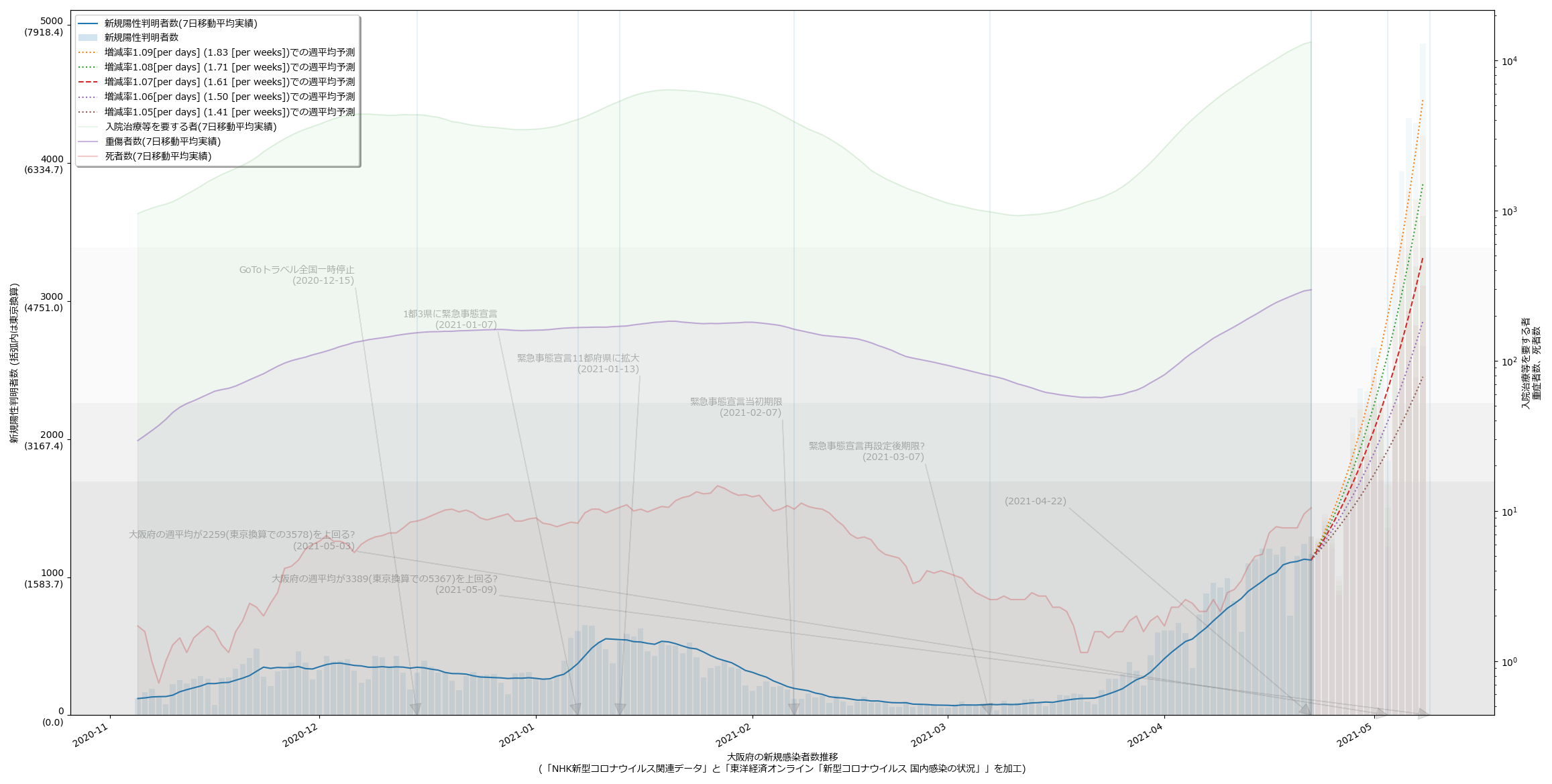
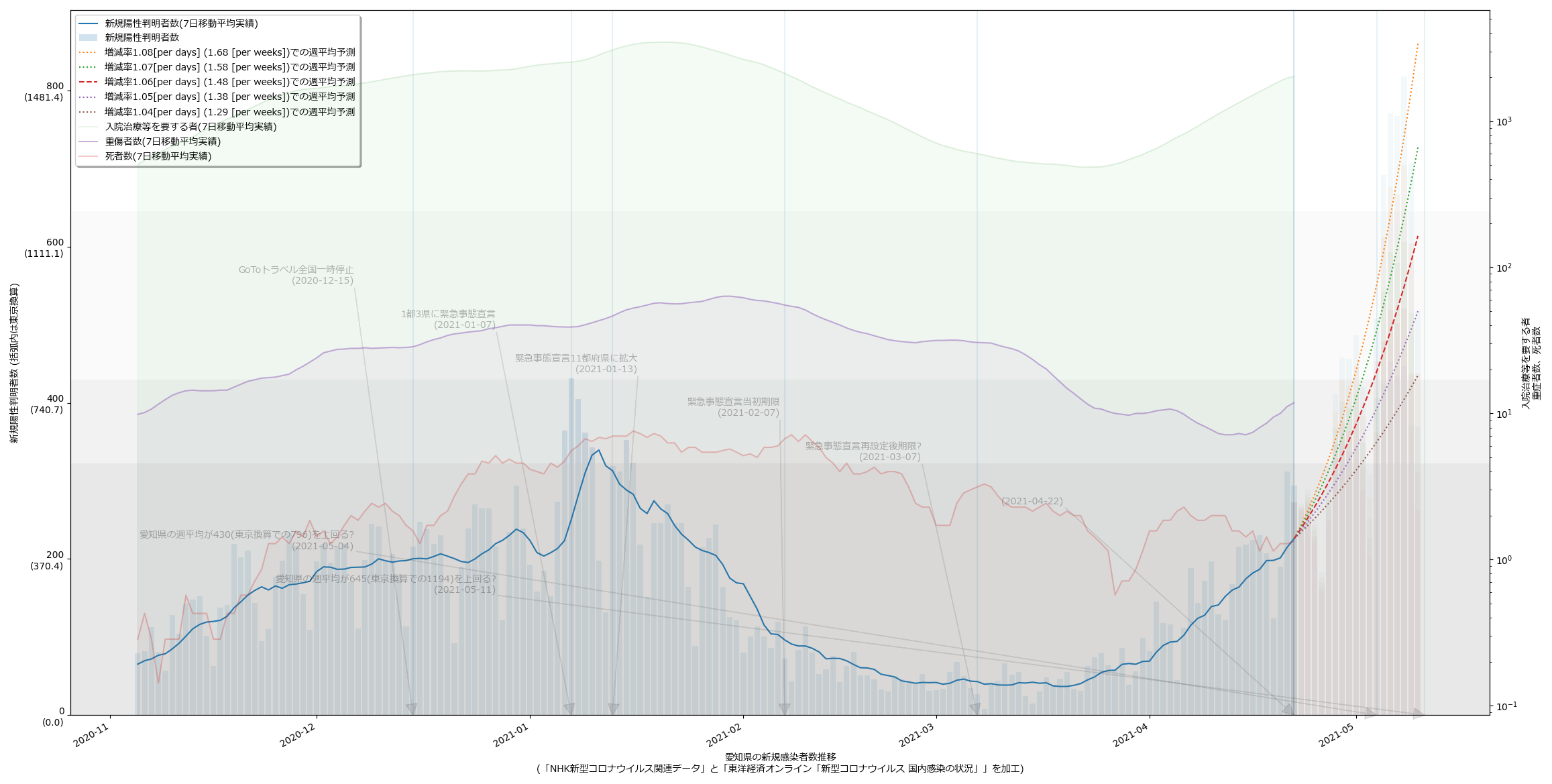
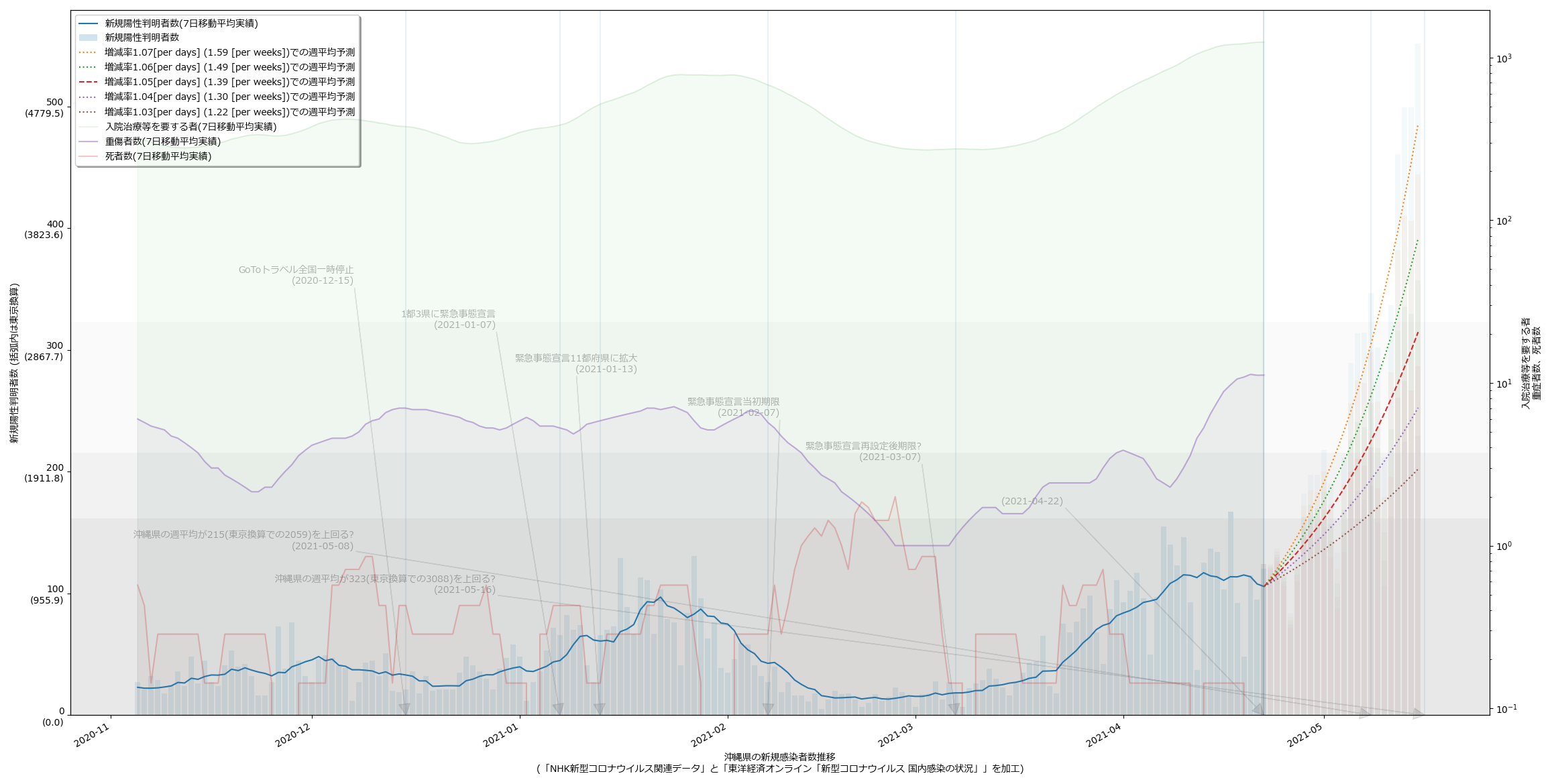
大阪はほんとは少しピークアウトの傾向が出てるんだけど、ワタシのアホ予測は「上がってる」ことしかみてない推定なので、上がり続けるおそろしげな予測になってる。東京換算で、の値を読んで叫んでみればいい。
あ、あと一応念のために言っておきたいんだけれど、「素人のアホ予測」と卑下して言っているけれど、これは「疫学や統計学的な知恵を持たずに単純な数学(算数)だけに基づいている」ということに過ぎず、実際これで使ってる予測は、たとえば東京都のモニタリング会議が使ってる方法と全く同じ、はず。単位が「日に102%」みたいにしてるから違って見えるかもしれないけれど、つまりは「明日に102% x あさってに明日の102%、しあさってにあさっての102%、…」つまりは「一週間後は本日の「1.02 x 1.02 x 1.02 x 1.02 x 1.02 x 1.02 x 1.02 ≒ 1.15」倍」、説明されれば小学生でもわかるかもしれないこの計算を、専門家もやっている、てこと。専門家は、これに加えてこの比「1.15」の推移をも予測しようと試みるからこそ「専門家」なのだし、そこまでは確かに我々素人は簡単には手が出せない。この意味での「ワタシのはアホ予測」なの。